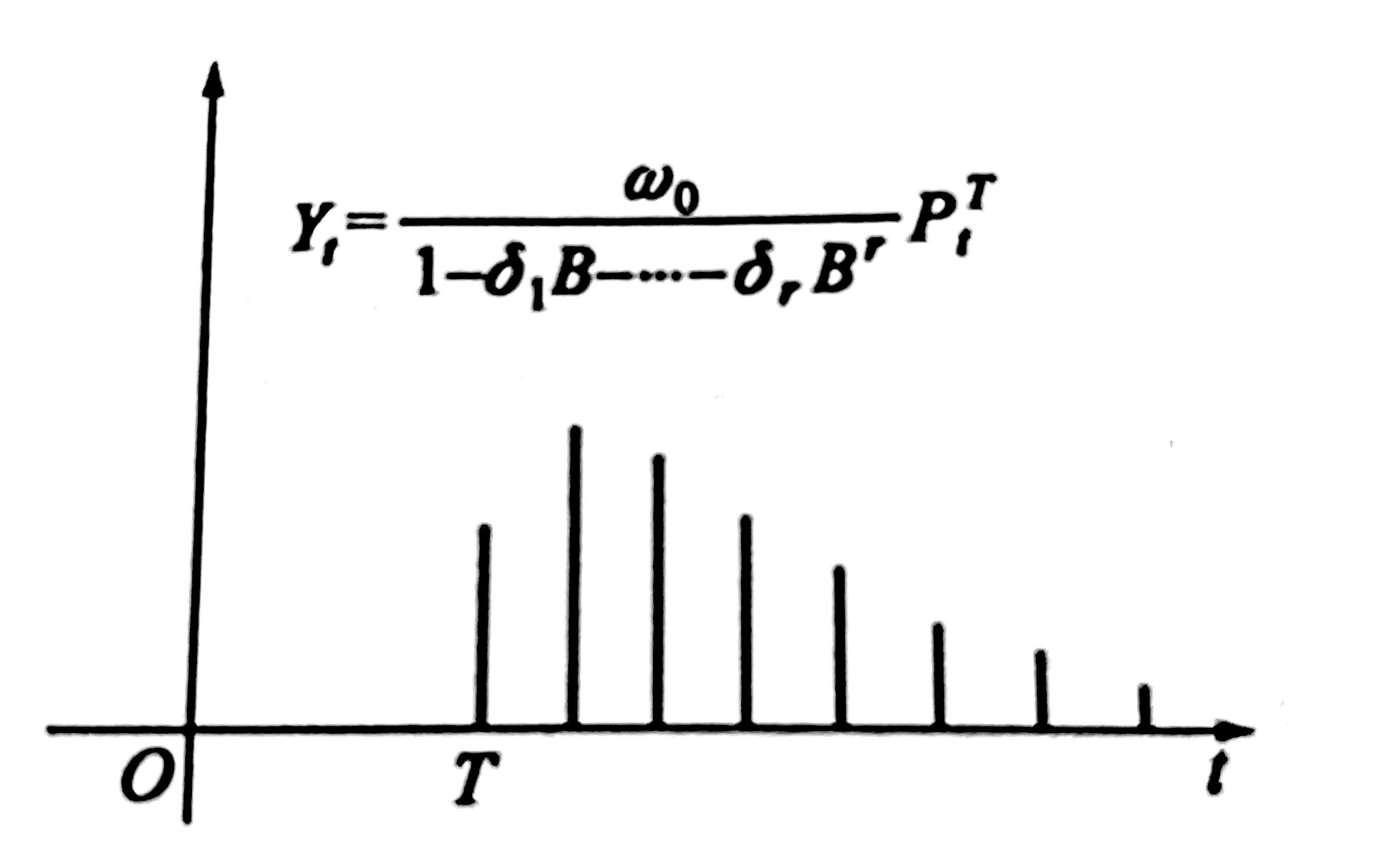传递函数与干预分析模型复习
复习传递函数与干预分析模型
参考书:经济预测与决策技术 武汉大学出版社 第四版
传递函数
传递函数的基本模型
设$Y_t=\nu(B)X_t+e_t$,这里
$Y_t$为输出序列,是因变量
$X_t$为输入序列,是解释变量
$e_t$为噪声。
$\nu(B)$是一个算子多项式,$B$是一个后移算子,$\nu_0,\nu_1,\cdots$称为脉冲响应权或传递函数的权,$e_t$是一个随机变量,其均值为0,方差固定,而且与$X_t,X_{t-1},\cdots$独立。
$X_t$在模型中不仅是解释变量,而且时间上对$Y_t$上来说,还是一个领先指标。例如,广告费用支出$X_t$将影响销售收入$Y_{t+k},Y_{t_k+1}$等等,也就是说,$X_t$对$Y_t$的影响提前$k$个时期。
但是算子多项式$\nu(B)$有无限多项,不符合节省的建模原则。对此,Jorgenson指出:在某些一般性的条件下,可以用算子$B$的两个有限的有理多项式之比来估计$\nu(B)$,即
$\nu(B)=\frac{\omega(B)}{\delta(B)}$
$\omega(B)=\omega_0-\omega_1 B - \cdots - \omega_s B^s$
$\delta(B)=1-\delta_1 B - \cdots - \delta_r B^r$
设$b$为$X_t$对$Y_t$影响的超前时期,那么传递函数模型就可以写成$Y_t=\frac{\omega(B)}{\delta(B)}X_{t-b}+e_t$
但是$e_t$不一定是白噪声,但是假定$e_t$是同解释变量$X_t$是统计独立的,因而用$ARMA(p,q)$模型去表示$e_t$是完全有可能的,即是有$\nabla^d e_t = \frac{\theta(B)}{\varphi(B)}a_t$,$\nabla^d$是$d$阶连续差分算子。
引入他的目的在于使$e(t)$满足平稳性,$a_t$是白噪声,$\varphi(B)$与$\theta(B)$分别满足平稳性与可逆性条件。
这样传递函数模型就可以写成:
$$y_t = \frac{\omega(B)}{\delta(B)}x_{t-b}+\frac{\theta(B)}{\varphi(B)}a_t$$
其中
$y_t=\nabla ^{d’}Y_t,x_t=\nabla ^d X_t$,均表示为平稳的随机过程。
$d’$是使$y_t$平稳的连续差分算子的阶数,$d$是使$X_t$平稳的连续差分算子的阶数。
并且为了满足平稳性与可逆性条件,$\omega_i(B),\delta_i(B),\varphi(B),\theta(B)$的跟均在单位圆外。
完整的传递函数模型如下:
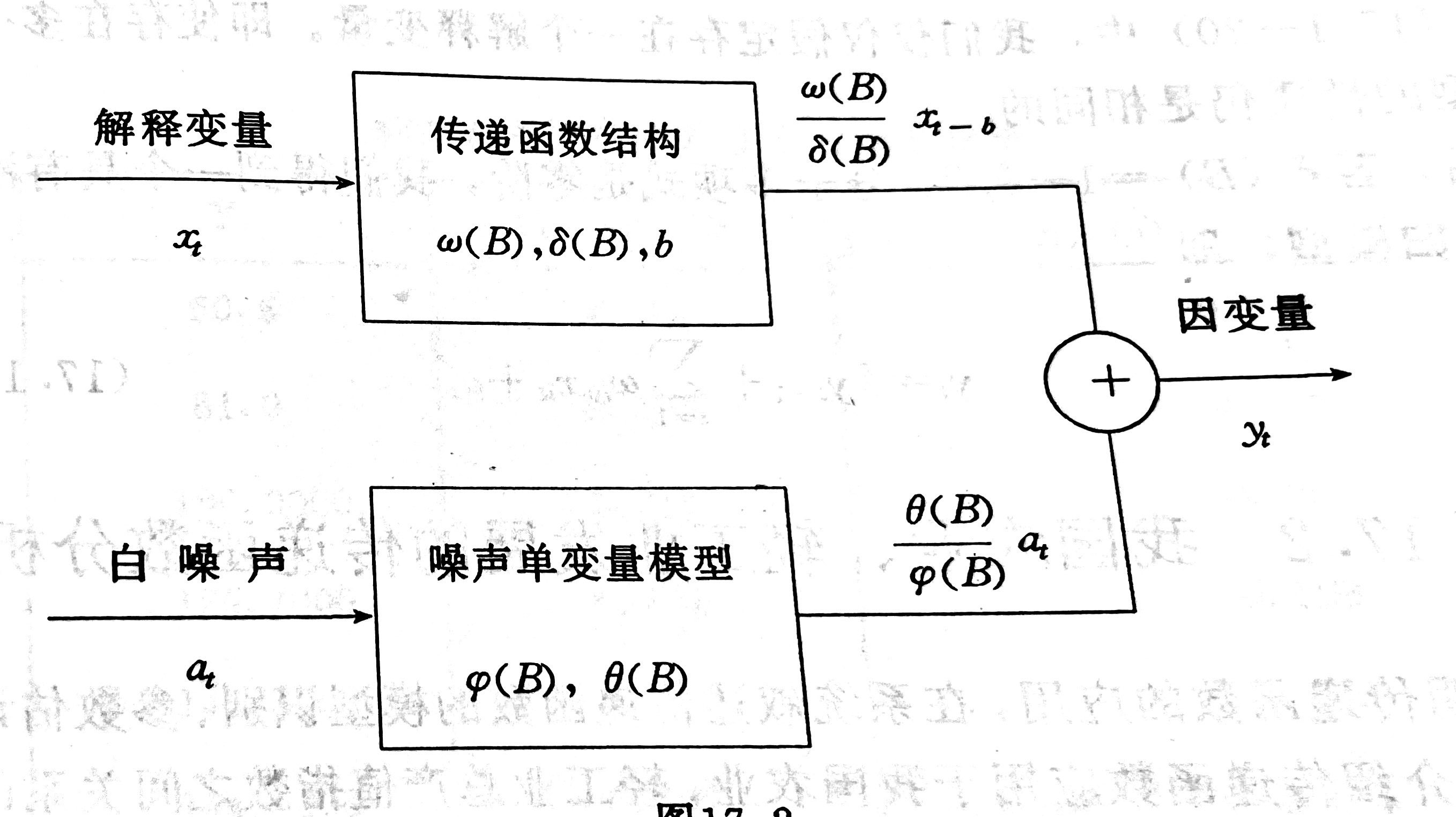
上述模型可以推广到含多个解释变量的情况,因而更一般的传递函数模型可以写成:
$$y_t=\sum\limits_{i=1}^m \frac{\omega_i(B)}{\delta_i(B)}x_{it-b}+\frac{\theta(B)}{\varphi(B)}a_t$$
这里$m$是解释变量的个数。同时假定$\omega_i(B),\delta_i(B),\varphi(B),\theta(B)$的根都在单位圆外。
互协方差与互相关函数的基本概念
设$x_t,y_t$是平稳序列,$x_t$是输入,$y_t$是输出。已知$Ex_t = m_x, Ey_t = m_y$
则称$r_{xy}(k)=E(x_t-m_x)(y_{t+k}-m_y)$为平稳序列$x_t$与$y_t$的互协方差函数。
互协方差函数和自协方差函数有很大的区别,例如互协方差函数$r_{xy}(k)$没有关于$k$的对称性,即$r_{xy}(k) \neq r_{xy}(-k)$
两平稳序列的互相关函数是由互协方差函数定义的,记为$\rho_{xy}(k)$
$$\rho_{xy}(k)=\frac{r_{xy}(k)}{\sigma_x \sigma_y} , k=0,\pm 1,\pm 2,\cdots$$
我们不仅关注理论上的两个变量之间的互协方差和互相关,更关心样本互协方差和互相关,样本互协方差定义为
$$\hat{r_{xy}}(k) = \begin{cases}
\frac{1}{n} \sum_{t=1}^{n-k} (x_t - \bar{x})(y_{t+k}-\bar{y}) & k=0,1,2,\cdots \\
\frac{1}{n} \sum_{t=1-k}^{n} (x_t - \bar{x})(y_{t+k}-\bar{y}) & k=-1,-2,\cdots \\
\end{cases}$$
这里$\bar{x},\bar{y}$是样本$x_t,y_t$的均值,$n$是原始数据经过差分运算化为平稳数据的有效观测数据数,由此,得到样本的互相关函数为
$$\hat{\rho_{xy}}(k)=\frac{\hat{r_{xy}}(k)}{S_xS_y}$$
其中$S_x,S_y$分别表示$x_t,y_t$的样本标准差
回忆:样本标准差$S=\sqrt{\frac{1}{n-1}\sum\limits_{k=1}^n(x_k - \bar{x})^2}$
一些互相关函数的例子
下面均假设$x_t,y_t$是零均值的平稳随机序列,以及输入$x_t$与未来噪声$e_{t+k}$不相关,即$Ex_te_{t+k}=0,k>0$。
eg1:设$x_t$是白噪声,满足$y_t = \omega_0x_{t-b}+e_t$,$e_t$是误差,$x_t$与未来的误差$e_{t+k}$无关,计算$x_t$和$y_t$的互协方差函数与互相关函数。
$r_{xy}(k)=Ex_ty_{t+k}=E x_t(\omega_0x_{t+k-b}+e_{t+k})=\omega_0Ex_tx_{t+k-b}$
由于$x_t$是白噪声,故协方差函数为:
$$r_{xy}(k)=\begin{cases}
\omega_0 \sigma_x^2 & k=b \\
0 & otherwise \\
\end{cases}$$
$\sigma_x^2$是$x_t$的方差,其互相关函数为
$$\rho_{xy}(k)=\begin{cases}
\omega_0 \frac{\sigma_x}{\sigma_y} & k=b \\
0 & otherwise \\
\end{cases}$$
eg2:计算$y_t=\frac{\omega_0}{1-\delta_1B}x_{t-b}+e_t$的互协方差和互相关
若$|\delta_1|<1$,可将此模型写成无穷序列和的形式
$$y_t=\omega_0\sum_{i=0}^\infty \delta_1^ix_{t-b-i}+e_t$$
则互协方差函数$r_{xy}(k)$可写成
$$r_{xy}(k)=Ex_t(\omega_0\sum_{i=0}^\infty \delta_1^ix_{t+k-b-i})$$
由于$x_t$与$e_{t+k}$无关,且$x_t$是白噪声,故
$$r_{xy}(k)=E(\omega_0 \sum_{i=0}^\infty \delta_1^i x_t x_{t+k-b-i}) = \omega_0E_tx_{t+k-b}+\omega_0 \delta_1 Ex_tx_{t+k-b-1} + \cdots $$
因此有
$$r_{xy}(k)=\begin{cases}
0 & k<b \\
\omega_0 \sigma_x^2 & k=b \\
\omega_0 \delta_1^j \sigma_x^2 & k=b+j, j>0 \\
\end{cases}$$
$$\rho_{xy}(k)=\begin{cases}
0 & k<b \\
\omega_0 \frac{\sigma_x}{\sigma_y} & k=b \\
\omega_0 \delta_1^j \frac{\sigma_x}{\sigma_y} & k=b+j, j>0 \\
\end{cases}$$
eg3:计算$y_t = \omega_0 x_{t-b} - \omega_1x_{t-b-1}+e_t$的互协方差和互相关
$r_{xy}(k)=Ex_t(\omega_0x_{t+k-b} - \omega_1 x_{t+k-b-1} + e_{t+k}) = \omega_0Ex_tx_{t+k-b} - \omega_1 Ex_t x_{t+k-b-1}$
因此有
$$r_{xy}(k)=\begin{cases}
\omega_0 \sigma_x^2 & k=b \\
-\omega_1 \sigma_x^2 & k=b+1 \\
0 & otherwise \\
\end{cases}$$
$$\rho_{xy}(k)=\begin{cases}
\omega_0 \frac{\sigma_x}{\sigma_y} & k=b \\
-\omega_1 \frac{\sigma_x}{\sigma_y} & k=b+1 \\
0 & otherwise \\
\end{cases}$$
eg4:计算$y_0=\frac{\omega_0-\omega_1B}{1-\delta_1B}x_{t-b}+e_t$的互协方差和互相关函数
上式可以拆为:$y_0 = \frac{\omega_0}{1-\delta_1B}x_{t-b} - \frac{\omega_1}{1-\delta_1B} x_{t-b-1} + e_t = \omega_0 \sum\limits_{i=0}^\infty \delta_1^i x_{t-b-i} + \omega_1 \sum\limits_{i=0}^\infty \delta_1^i x_{t-b-i-1} + e_t$
$r_{xy}(k)=E\omega_0x_t\sum\limits_{i=0}^\infty \delta_1^i x_{t+k-b-i} - E\omega_1x_t \sum\limits_{i=0}^\infty x_{t+k-b-i-1}$
因此有
$$r_{xy}(k)=\begin{cases}
0 & k<b \\
\omega_0 \sigma_x^2 & k=b \\
\omega_0 \delta_1 \sigma_x^2-\omega_1 \sigma_x^2 & k=b+1 \\
\omega_0 \delta_1^j\sigma_x^2 - \omega_1 \delta_1^{j-1}\sigma_x^2 & k=b+j,j>0
\end{cases}$$
$$\rho_{xy}(k)=\begin{cases}
0 & k<b \\
\omega_0 \frac{\sigma_x}{\sigma_y} & k=b \\
\omega_0 \delta_1 \frac{\sigma_x}{\sigma_y}-\omega_1 \frac{\sigma_x}{\sigma_y} & k=b+1 \\
\omega_0 \delta_1^j\frac{\sigma_x}{\sigma_y} - \omega_1 \delta_1^{j-1}\frac{\sigma_x}{\sigma_y}& k=b+j,j>0
\end{cases}$$
传递函数模型的识别步骤
step1:对原始的输入输出序列进行平稳性处理
step2:白化输入序列与漂白输出序列
step3:计算白化序列$\alpha_t$与漂白序列$\beta_t$的互相关
step4:估计脉冲响应权
step5:对$(r,s,b)$的识别
step6:噪声序列$e_t$的计算
step7:对噪声序列$e_t$进行识别,建立$ARMA(p,q)$模型
干预模型分析
干预分析模型的基本变量都是干预变量,它由阶跃函数和点函数表示,即
$$S_t^T =\begin{cases}
0 & 干预事件发生之前,即当t<T时 \\
1 & 干预事件发生之后,即当t \ge T时
\end{cases}$$
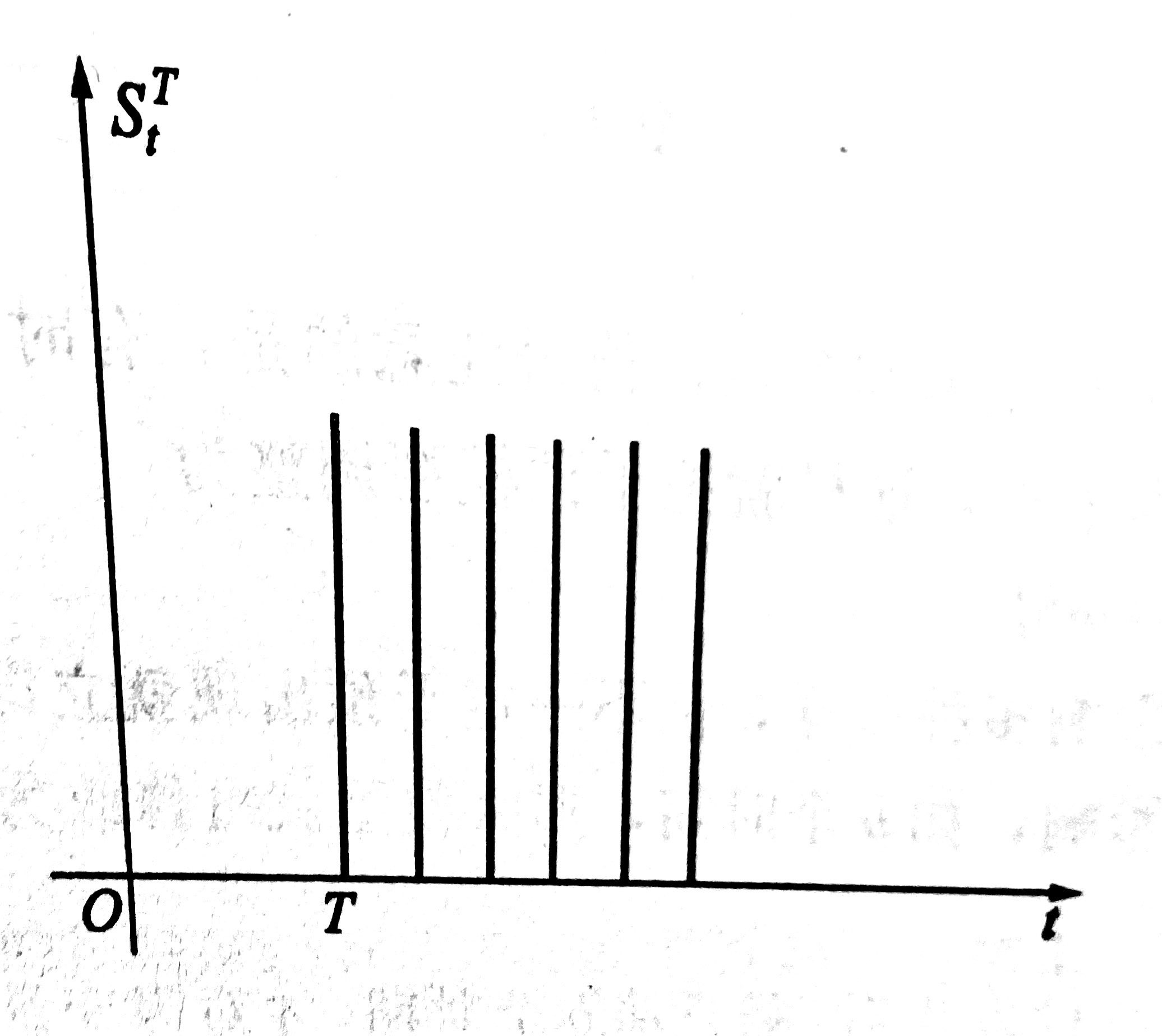
这种干预变量一旦发生,就会长期产生影响,故称这种变量为持续的干预变量。
但是,有些干预影响只有暂时性,而无持续性
例如:某种促销广告,进在某一段时间内影响销售量,这种干预变量可表示为:
$$P_t^T =\begin{cases}
0 & 干预事件发生之前,即当t=T时 \\
1 & 干预事件发生之后,即当t \ne T时
\end{cases}$$
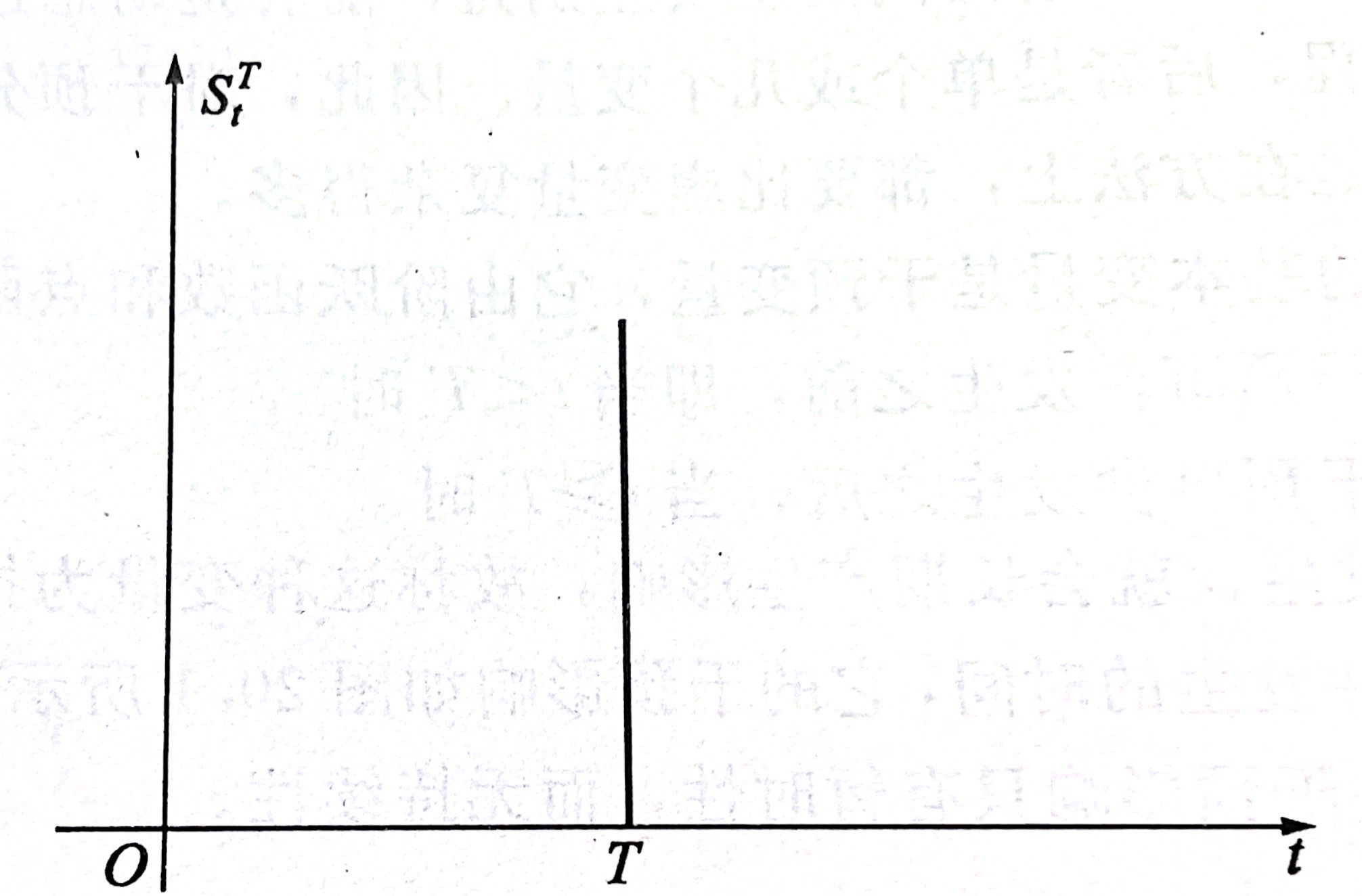
上述两类干预变量虽然表示形式不同,但是他们之间有如下的内在联系,即$(1-B)S_t^T = P_t^T$
这里的$B$是后移算子,有$BS_t^T = S_{t-1}^T$
干预事件的影响突然开始,长期持续下去的模型:
设干预对因变量的影响是固定的,从某一时刻$T$开始,但影响的程度是未知的,单因变量的大小是位置的。这种影响可以概括为以下的干预模型:
$$Y_t = \omega S_t^T$$
这里的$Y_t$是干预的输出,$\omega$是位置参数。值得注意的是有的时候$Y_t$不一定是平稳的,而且要求通过差分化为平稳,这样就把干预模型调整为
$$(1-B)Y_t = \omega S_t^T$$
有的时候不一定干预出现就立即产生影响,甚至要滞后若干个时期才产生影响,如$b$个时期,那么模型就可以修改为
$$Y_t = \omega B^bS_t^T$$
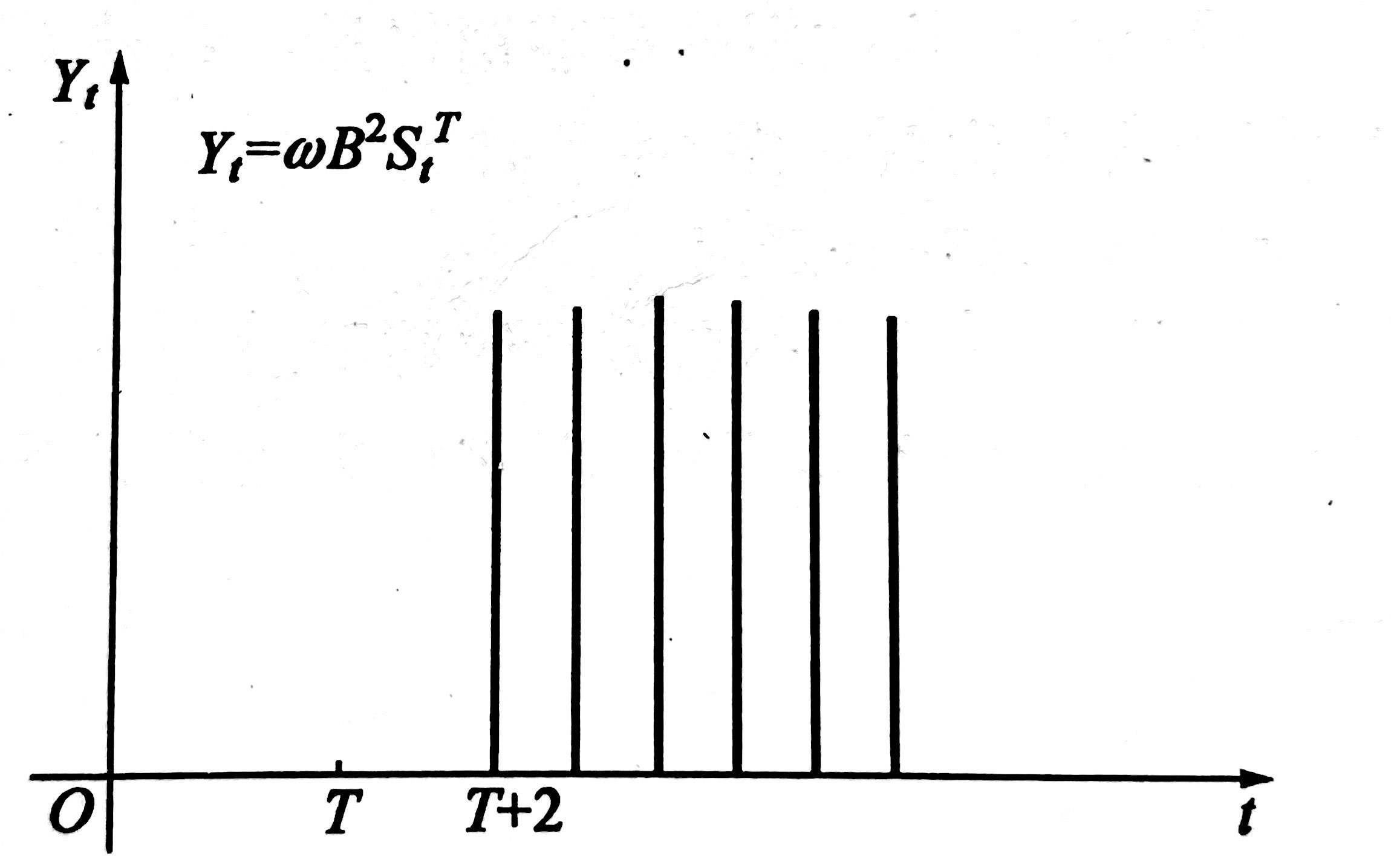
干预事件的影响逐渐开始,长期持续下去
有的时候干预事件突然发生,并不能立刻产生完全的影响,而是随着时间的推移,逐渐地感到这种影响的存在,其模型方程如下:
$$Y_t = \frac{\omega B}{1-\delta B}S_t^T$$
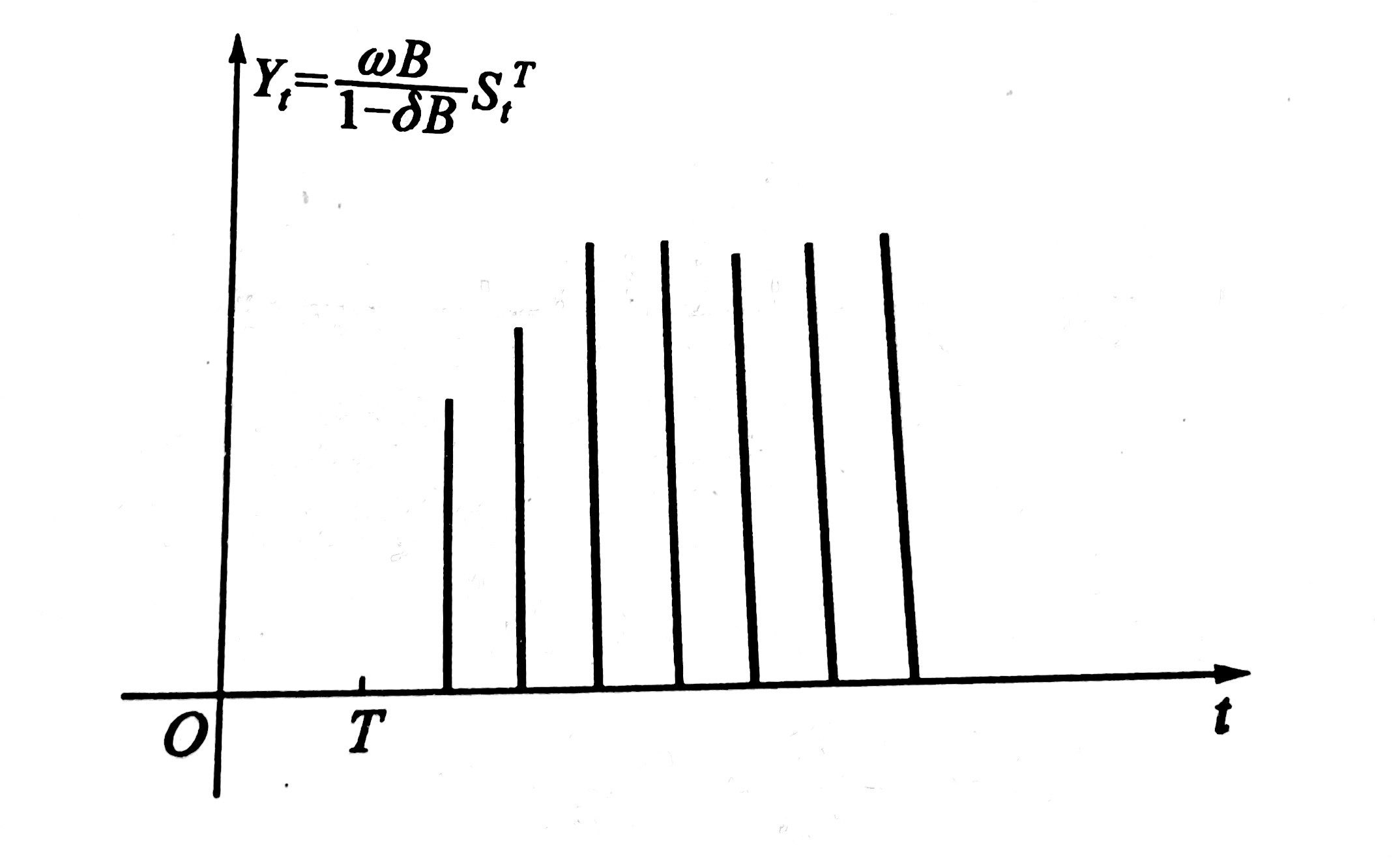
更一般的模型是:
$$Y_t = \frac{\omega B^b}{1-\delta_1B - \cdots - \delta_rB^r} S_t^T$$
干预突然开始带来暂时的影响
在广告对销售量的实例中,我们注意到如下事实:在广告促销活动开始后的第某个月,例如在第$b$个月,销售量突然上升,此后影响逐渐减弱,直到消失,这类干预现象可以用数学模型描述如下:
$$Y_t = \frac{\omega B^b}{1-\delta B} P_t^T$$
当$\delta=0$的时候,干预的影响只存在一个时期;当$\delta=1$时,干预的影响将长期存在。
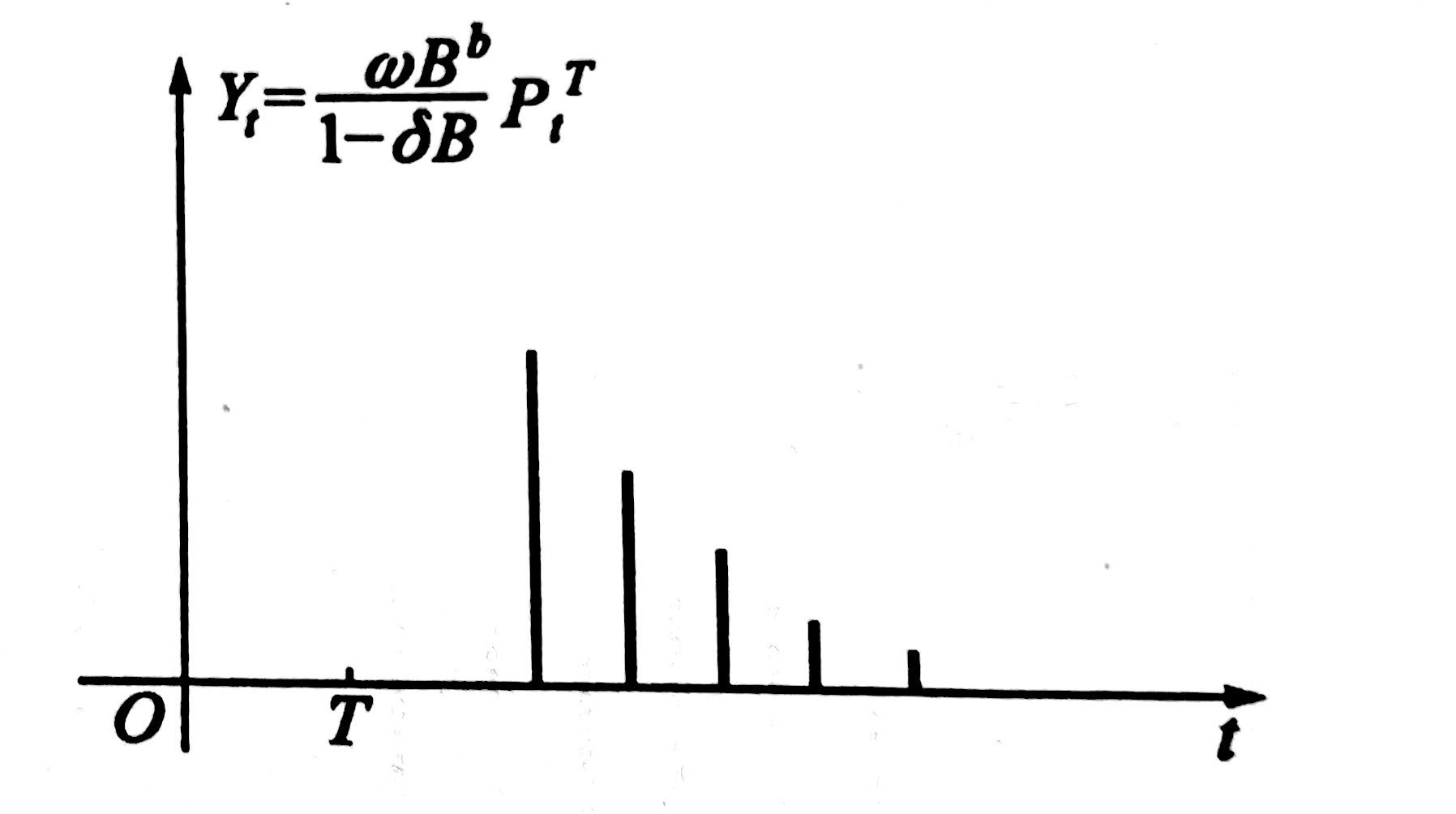
若在逐渐地降低冲击影响之后期望一个持久的影响,干预模型则有如下的形式:
$$Y_t = (\frac{\omega_1 B}{1-\delta B} + \frac{\omega_2 B}{1-B}) P_t^T$$
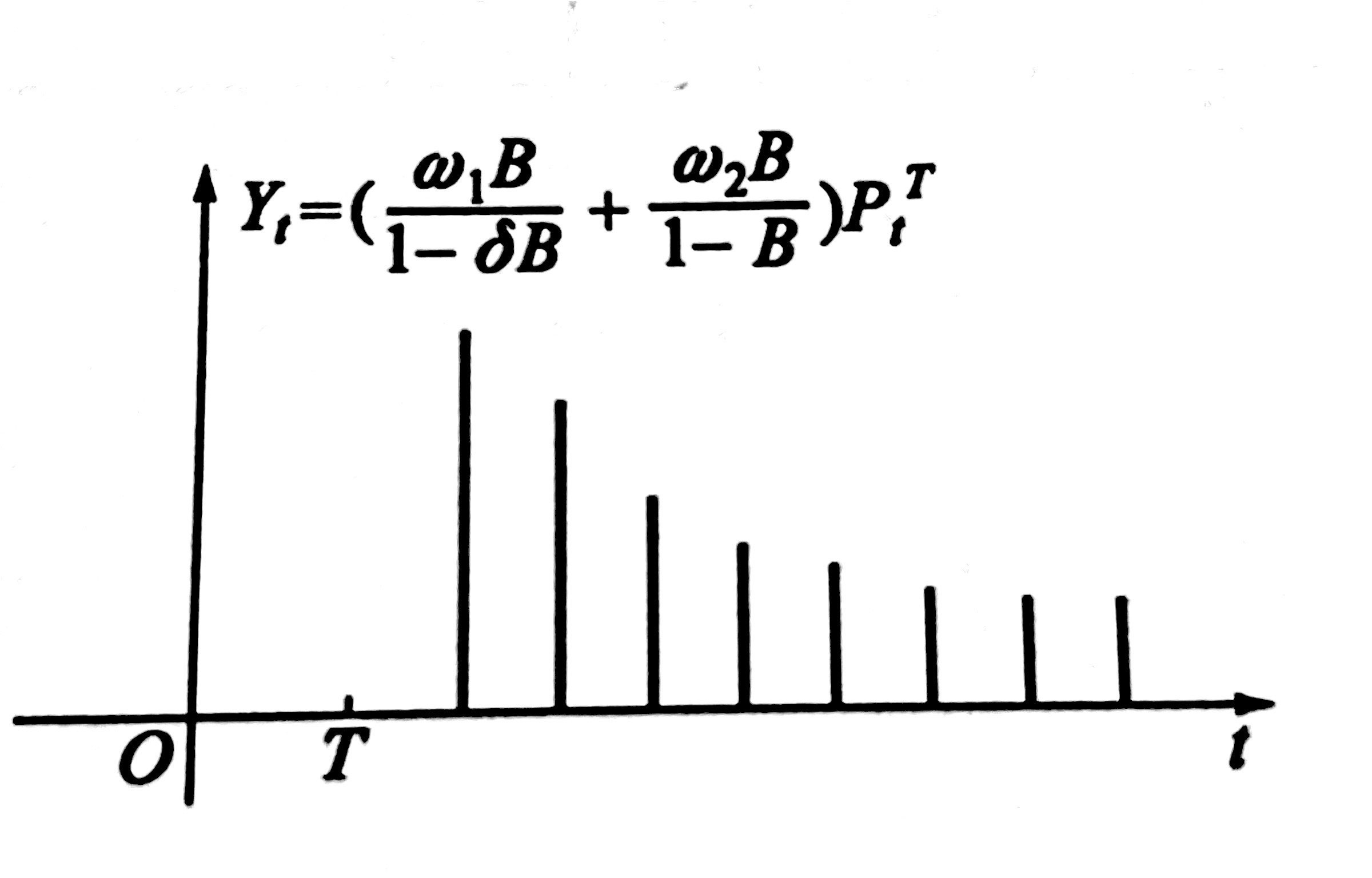
干预逐渐开始产生短暂的影响
干预的影响逐渐增加,在某个时刻达到高峰,然后又逐以减弱以致消失。这类干预现象可以用以下模型去描绘:
$$Y_t = \frac{\omega_0}{1-\delta_1B - \cdots - \delta_r B^r} P_t^T$$
$r$的值一般大于等于2,因为$r=1$不能描绘和模拟此模型。