经济决策技术复习
复习经济决策技术
参考书:经济预测与决策技术 武汉大学出版社 第六版
决策学概论
决策的概念及决策应遵循的基本原则:
我们认为决策有狭义和广义之分。狭义地理解就是通常所讲的对未来事物所做的决定,仅限于对不同方案选出最佳方案;广义地理解就是把决策看作一个管理过程,是人们为了实现特定的目标,运用科学的理论与方法,系统地分析主客观条件,提出各种预选方案,从中选出最佳方案,并对最佳方案的实施进行监控,掌握决策的实施情况,强调系统的优化。
不管是狭义的决策还是广义的决策,都主张决策必须遵从一些基本的原则。这些原则是:
最优化原则
系统原则
信息准全原则
可行性原则
集团决策原则
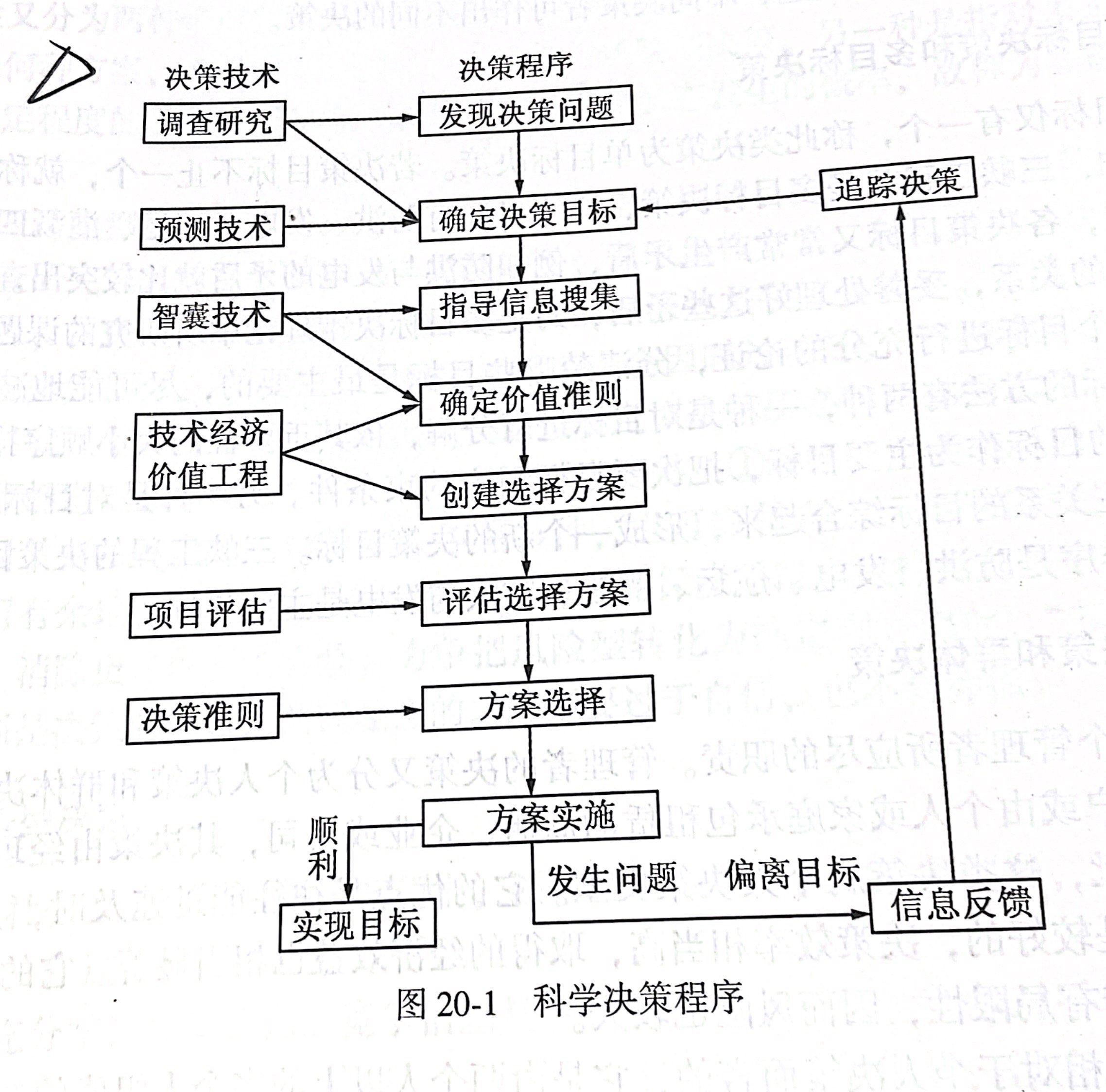
科学的决策程序
决策的步骤基本如下:
发现决策问题
确定决策目标
指导信息搜集
确定价值标准
创建可供选择的方案
评估选择方案
选择最佳方案进行决策
方案实施,控制决策的执行情况
信息反馈,必要时实行追踪决策
决策的基本类型
决策所要解决的以及所面临的问题是多方面的,因此,有不同类型的决策。归纳起来有以下几种类型。
战略决策与战术决策
规范性决策和非规范性决策
单目标决策和多目标决策
个人决策和群体决策
确定型决策与非确定型决策
竞争性决策
非确定型决策
不确定型决策
我们对于例子来分析每种决策
悲观决策法和乐观决策法

悲观决策法说的是在每种情况中取最坏的可能后再取收益最大的一种。
在上述例子中,三种情况最坏的收益分别为$-6,0,10$,再取最大的应该选择$D_3$
乐观决策法说的是在每种情况中取最好的可能后再取收益最大的一种。
在上述例子中,三种情况最好的收益分别为$60,30,10$,再取最大的应该选择$D_1$
PERT决策法
在策略$D_i$下,最乐观的盈利为$x_i$元,最保守的盈利为$y_i$元,最可能的盈利为$z_i$元。则期望获益的计算公式为:$$E(D_i)=\frac{x_i+4z_i+y_i}{6}$$

在上图中,设“畅销”对应于最乐观,“滞销”对应于最保守,“平销”对应着最可能,则
$$E(D_1)=\frac{60+4\times 10-6}{6}=15.7, E(D_2)=22.66,E(D_3)=10$$
取最大的即为$D_2$
赫威兹(Hurwicz)决策法(乐观系数决策法)
这种方法的基本步骤是对未来情况保持一定的乐观态度,但也不要盲目乐观,乐观程度大小以一个乐观系数$\alpha(0< \alpha < 1)$表示,$\alpha$越接近1,则代表越乐观。各种策略的期望收益可以按照下述公式计算:
$$E(D_i)=最高获益\times \alpha + 最低获益\times (1-\alpha)$$

决策准则是期望获益最大者为最优策略,上图最优策略即为$D_1$
小中取大决策法(Wald决策准则)
这种决策方法指导思想是,一切从最坏的情况出发去选取方案。然后,在个方案最坏的决策后果中,找出一种较好的结果。

在上图中,$D_1,D_2,D_3$的最低获益是${-6,0,10}$,从中取最大的即为$10$,对应的为$D_3$
最小最大后悔值法
就是选择让最大后悔值达到最小的方案。
具体步骤为:
(1)列出市场各种情况的最高获益。
(2)计算出市场各种情况的后悔值,即用各项最高收益减去该项原来的估计值。
(3)求出各项的最大后悔值,$D_1$对应$16$,$D_2,D_3$分别对应$30,50$,在从中选出最小的,即$D_1$对应的$16$,那么$D_1$就是最优策略。

| 市场情况 | 畅销 | 平销 | 滞销 |
|---|---|---|---|
| 最高获益 | $60$ | $25$ | $10$ |
| 策略 | 畅销 | 平销 | 滞销 |
|---|---|---|---|
| $D_1$ | $60-60=0$ | $25-10=15$ | $10-(-6)=16$ |
| $D_2$ | $60-30=30$ | $25-25=0$ | $10-0=10$ |
| $D_3$ | $60-10=50$ | $25-10=15$ | $10-10=0$ |
等概率决策法
我们虽然不知道每种情况的概率,但是我们把每种市场状态发生的可能性看作是完全相等的,由此导出的决策方法,成为等概率决策法。

我们设畅销、平销和滞销的概率均为$1/3$,那么可以计算出$D_1,D_2,D_3$三种情况的期望盈利
$$ED_1=\frac{1}{3}\times 60 +\frac{1}{3} \times 10 + \frac{1}{3} \times (-6) \approx 22.33$$
$$ED_2=\frac{1}{3} \times 30 + \frac{1}{3} \times 25 + \frac{1}{3} \times 0 \approx 18.33$$
$$ED_3=\frac{1}{3} \times 10 + \frac{1}{3} \times 10 + \frac{1}{3} \times 10 = 10$$
期望最大$D_1$的即为最优策略。
风险型决策
决策树技术
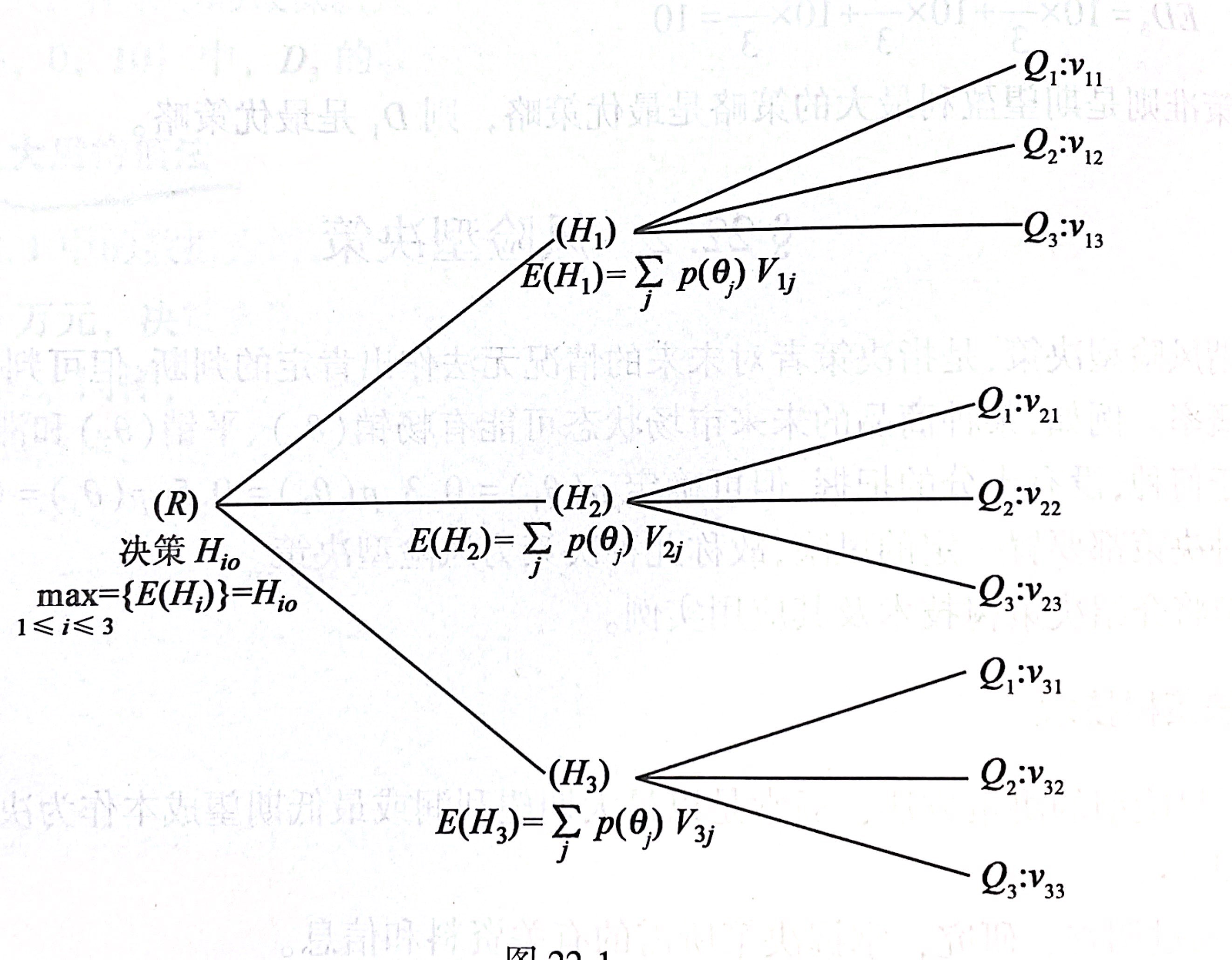
上图中$(R)$代表决策点,称为树根,$(H_i),i=1,2,\cdots , n$代表策略点。从$(R)$出发引出的$n$条线称为树枝或者策略枝。从策略点$(H_i)$引出的$m$条线,表示$m$种自然状态,出现第$j$种状态的概率计为$p_j,j=1,2,\cdots, m$,称这$m$条线为概率枝。$v_{ij}$表示采用第$i$种策略的获利(或成本),则可计算各种策略(或方案)的期望获利(或成本),计算公式为$E(H_i)=\sum_{i=1}^mp_jv_{ij}$
由期望利益最大决策准则,得到最优策略是使${E(H_i)}$取最大值的$H_{i_0}$,即$ \max\limits_{1 \leq i \leq n} E(H_i)=E(H_{i_0})$
若决策准则是期望成本最小,则最优策略是使${E(H_i)}$取最小值的$H_{i_0}$,即$ \min\limits_{1 \leq i \leq n} E(H_i)=E(H_{i_0})$
例题:
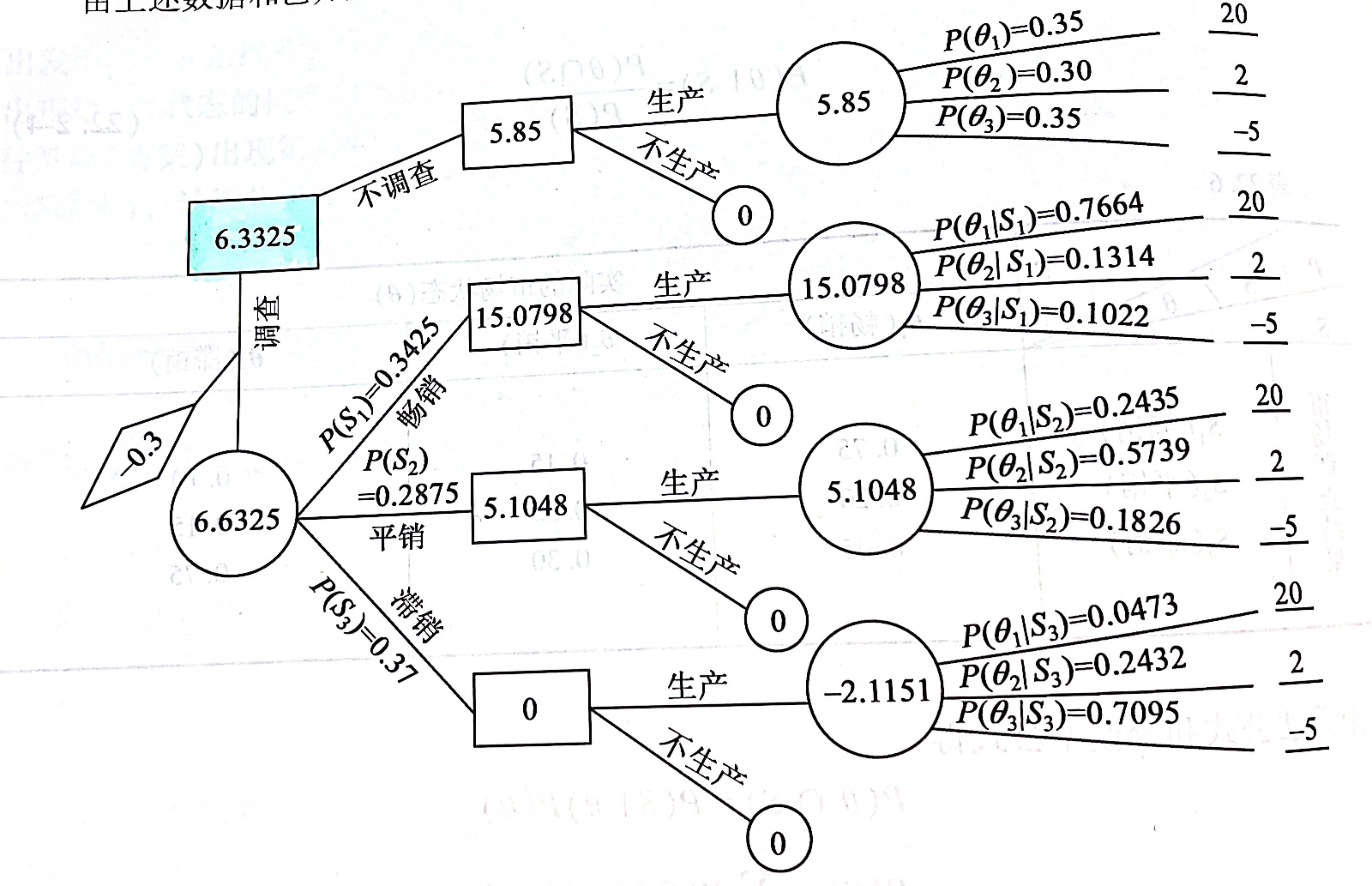
设某企业准备生产一种新产品,在决策前估计市场状态可能有畅销$(\theta_1)$,平销$(\theta_2)$,滞销$(\theta_3)$,由历史资料统计,$P(\theta_1)=0.35$,$P(\theta_2)=0.3$,$P(\theta_3)=0.35$,各种市场的盈利状态分别为20万元,2万元和-5万元。如果要做市场调查则要花0.3万元,预估的结果如表:
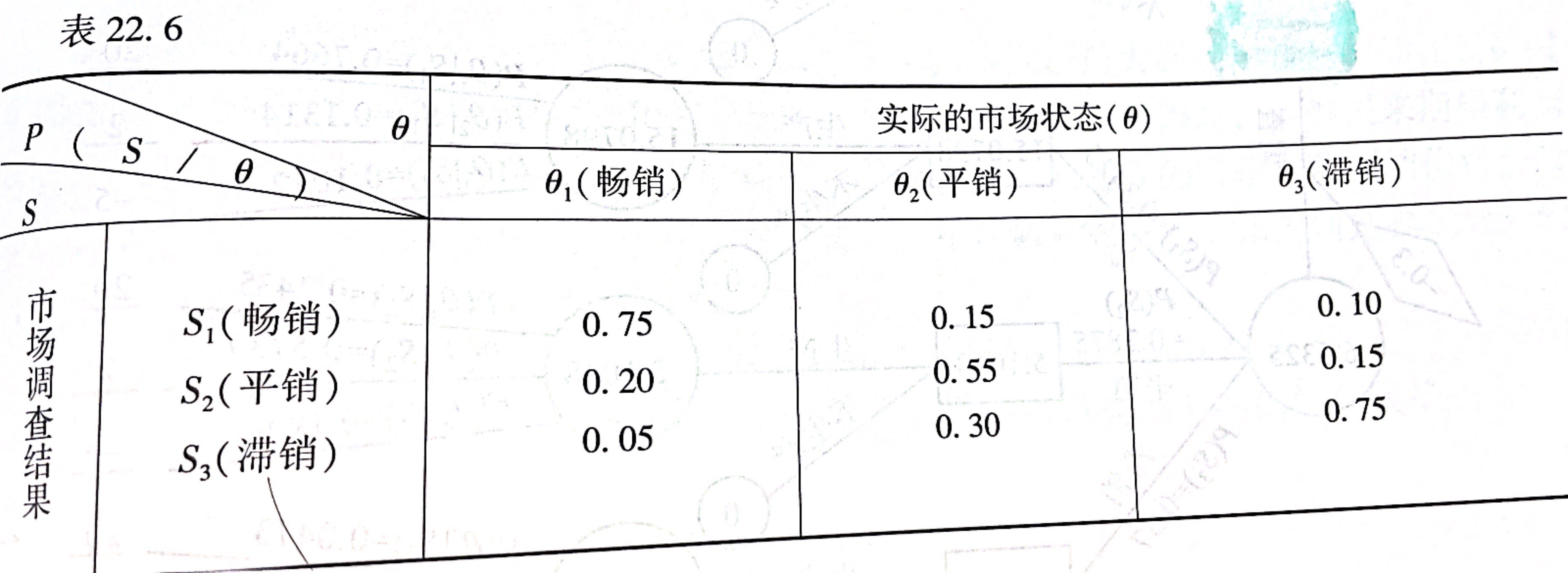
表中$P(S|\theta)$表示实际市场状态为$\theta$的条件下,调查结果为$S$的概率。例如,$P(S_1|\theta_1)=0.75$,表示在实际的市场状态是“畅销”,而调查结果状态为“畅销”的概率为$0.75$。但是,具有决策意义的是在调查结果为$S$的状态下,实际结果为$\theta$的概率$P(\theta |S)$。有条件概率公式得:
$$P(\theta |S ) = \frac{P(\theta \cap S)}{P(S)}, ~~ P(\theta \cap S)=P(S|\theta)P(\theta), ~~ P(S)=\sum_{i=1}^3P(\theta_i)P(S|\theta_i)$$
将表中的数据带入上述公式计算,可得到$P(\theta \cap S)$与$P(S)$的值,再可以算出$P(\theta |S)$
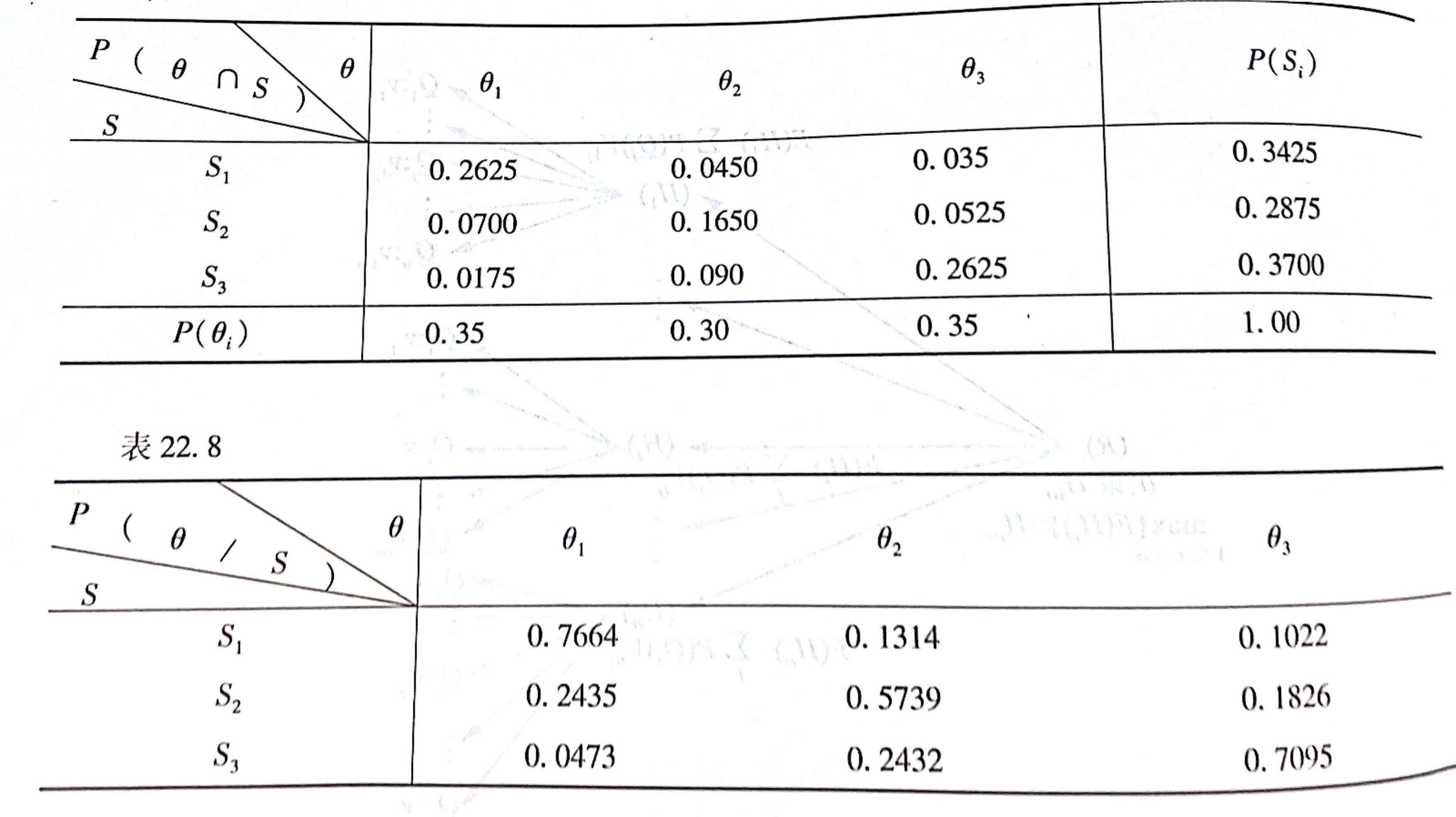
由上述数据与已知条件,可作出决策树(绿色的为树根结点)
概率排序型决策
有若干种自然状态$S_1,S_2,\cdots , S_n$
概率:$p_1,p_2,\cdots , p_n$
后果值:$\theta_{i1},\theta_{i2},\cdots, \theta_{in}$
各自概率若满足$p_1 \ge p_2 \ge \cdots \ge p_n $,或者$p_j-p_{j+1} \ge 0 ~ (j=1,2,\cdots,n-1)$,则称为概率弱排序
若能确定$M_j \ge 0 $,使得$p_j-p_{j+1} \ge M_j$,且至少有一个$M_j$大于$0$,则我们称为概率严排序。
在这种排序下,我们可以求出期望后果值的最大值与最小值,并以此作为决策的依据。
概率弱排序决策
假设对于某个方案$A$,它在自然状态$S_j$下的后果值为$\theta_j$,于是,该方案的期望收益为$\sum\limits_j p_j\theta_j$,求解该方案的期望的最大/最小后果就可以转化为如下的线性规划问题:
$$
\begin{cases}
\min or \max & E(A)=\sum\limits_j p_j\theta_j \\
s.t. & p_j - p_{j+1} \ge 0 \\
& \sum\limits_j p_j = 1 \\
& p_j \ge 0
\end{cases}
$$
令
$$q_j = p_j - p_{j+1} , j=1,2,\cdots n-1, q_n = p_n$$
$$y_j = \sum_{k=1}^{j}\theta_j$$
则线性规划可以转化为:
$$
\begin{cases}
\min or \max & E(A)=\sum\limits_j q_jy_j \\
s.t. & \sum\limits_j jq_j = 1 \\
& q_j \ge 0
\end{cases}
$$
该问题的基解为某个$q_k$为非零,其余$q_j$均非零。那么有$q_k = \frac{1}{k}$
$$E(A)=\frac{y_k}{k}=\frac{\theta_1 + \theta_2 + \cdots + \theta_k}{k} = \bar{\theta_k}$$
求出$\bar{\theta_k}$的最小、最大值即可。
例子:
某物品销售量和概率排序如下:
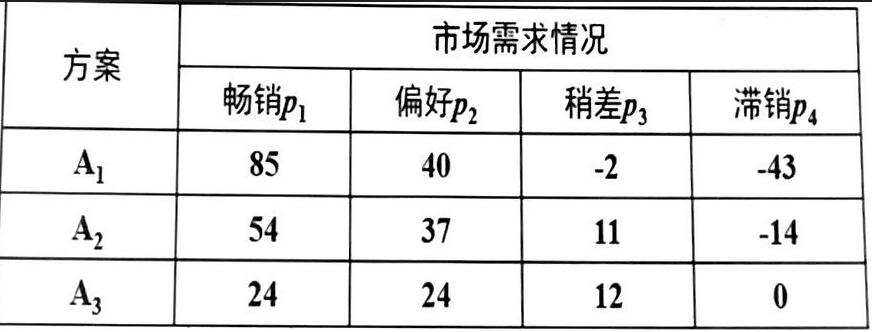
按照概率排序后,我们有
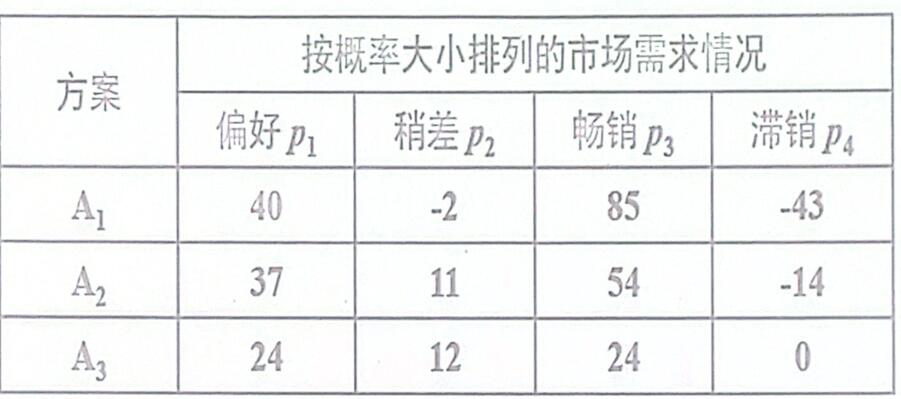
对于$A_1$,我们可以算出
$\bar{\theta_1}=\frac{40}{1} = 40$
$\bar{\theta_2}=\frac{40+(-2)}{2} = 19$
$\bar{\theta_3}=\frac{40+(-2)+85}{3} = 41$
$\bar{\theta_4}=\frac{40+(-2)+85+(-43)}{4} = 20$
同理可以算出其他结果如图:
| 方案/销量 | $\bar{\theta_1}$ | $\bar{\theta_2}$ | $\bar{\theta_3}$ | $\bar{\theta_4} $ | 概率弱排序下的$\max E(A) , \min E(A)$ |
|---|---|---|---|---|---|
| $A_1$ | $40$ | $19$ | $41$ | $20$ | $41,19$ |
| $A_2$ | $37$ | $24$ | $34$ | $22$ | $37,22$ |
| $A_3$ | $24$ | $18$ | $20$ | $15$ | $24,15$ |
概率严排序决策
线性规划可变为:
$$
\begin{cases}
\min or \max & E(A)=\sum\limits_j p_j\theta_j \\
s.t. & p_j - p_{j+1} \ge M_j \\
& \sum\limits_j p_j = 1 \\
& p_j \ge 0
\end{cases}
$$
做变换
$$r_j = p_j - p_{j+1} -M_j , j=1,2,\cdots , n-1 , ~ r_n = p_n$$
$$y_j = \sum_{k=1}^{j}\theta_j$$
$$C=\sum_j M_jy_j, ~~ D = \sum_j jM_j $$
则规划可以转化为
$$
\begin{cases}
\min or \max & E(A)=\frac{1-D}{k}y_k + C \\
s.t. & \sum\limits_j jr_j = 1 - D \\
& r_j \ge 0
\end{cases}
$$
可以推出
$$\min ~~ (\max) ~~ E(A)(严)= (1-D) \min ~~ (\max) ~~ E(A)(弱) + C$$
仍用上例,给出概率严排序$p_1 - p_2 \ge 0.15 , ~~ p_2 - p_3 \ge 0.3 , ~~ p_3 - p_4 \ge 0$,即$M_1 = 0.15,M_2 = 0.3, M_3 =0 $
对于方案$A_1$可以算出
$$C=M_1y_1 + M_2y_2 + M_3y_3 = 40 \times 0.15 + 38 \times 0.3 + 123 \times 0 = 17.4$$
$$D=M_1 + 2M_2 + 3M_3 = 0.15 + 2\times 0.3 + 3 \times 0 = 0.75$$
$$\bar{\theta_1}= 40, \bar{\theta_2}= 19, \bar{\theta_3}= 41, \bar{\theta_4}= 20$$
进而
$$(1-D)\bar{\theta_1}+C = 0.25 \times 40 + 17.4 = 27.4$$
$$(1-D)\bar{\theta_2}+C = 0.25 \times 19 + 17.4 = 22.15$$
$$(1-D)\bar{\theta_3}+C = 0.25 \times 41 + 17.4 = 27.65$$
$$(1-D)\bar{\theta_4}+C = 0.25 \times 20 + 17.4 = 22.4$$
可以看出在概率严排序下:$\max E(A)=27.65 , \min E(A) = 22.15$
| 方案/销量 | $\bar{\theta_1}$ | $\bar{\theta_2}$ | $\bar{\theta_3}$ | $\bar{\theta_4} $ | 概率严排序下的$\max E(A) , \min E(A)$ |
|---|---|---|---|---|---|
| $A_1$ | $40$ | $19$ | $41$ | $20$ | $27.65,22.15$ |
| $A_2$ | $37$ | $24$ | $34$ | $22$ | $29.2, 25.45$ |
| $A_3$ | $24$ | $18$ | $20$ | $15$ | $20.4,18.15$ |
利用期望值极值进行决策
从$A_1$与$A_2$进行比较来看,从非确定型,到概率弱排序,再到概率严排序,我们得到的信息值越来越多,也可以发现$A_1$的优势越来越不明显。最后到概率严排序时,$A_2$的优势已经高于$A_1$。
优势条件
严优势条件
$E(A_1)>E(A_2)$的充要条件是$\min E(A_1-A_2)>0$
令$D_1=A_1-A_2,D_2 = A_2-A_3,D_3 = A_1-A_3$,

计算出结果如下:
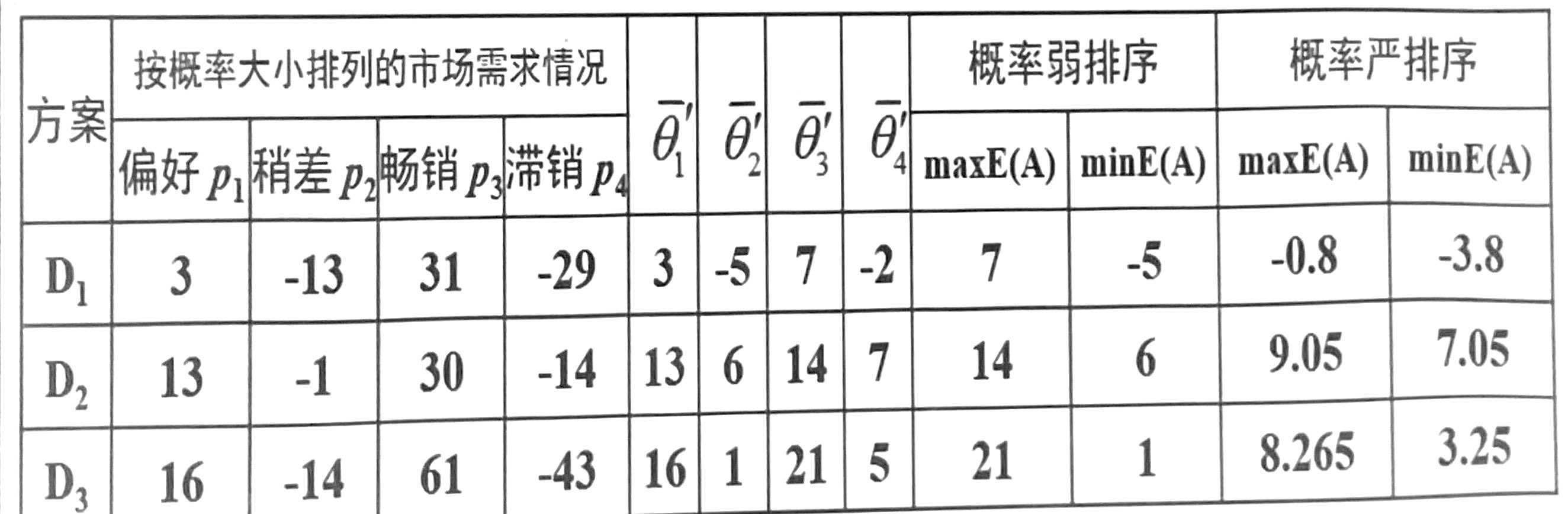
可以看出$\min E(D_2) > 0 , ~~ \min E(D_3) > 0$,所以方案$A_2,A_1$对方案3都有严优势
另外,$\max E(D_1) < 0$,所以$\min E(A_2 - A_1) = -\max E(D_2) >0$
因此在概率严排序的规则下,$A_2对A_1$也有严优势。
最优方案即为$A_2$
弱优势条件
对于方案$D=A_1-A_2$和$D’=A_2-A_1$
若$\max E(D) > \max E(D’)$,则称方案$A_1$对方案$A_2$有弱优势。
例子
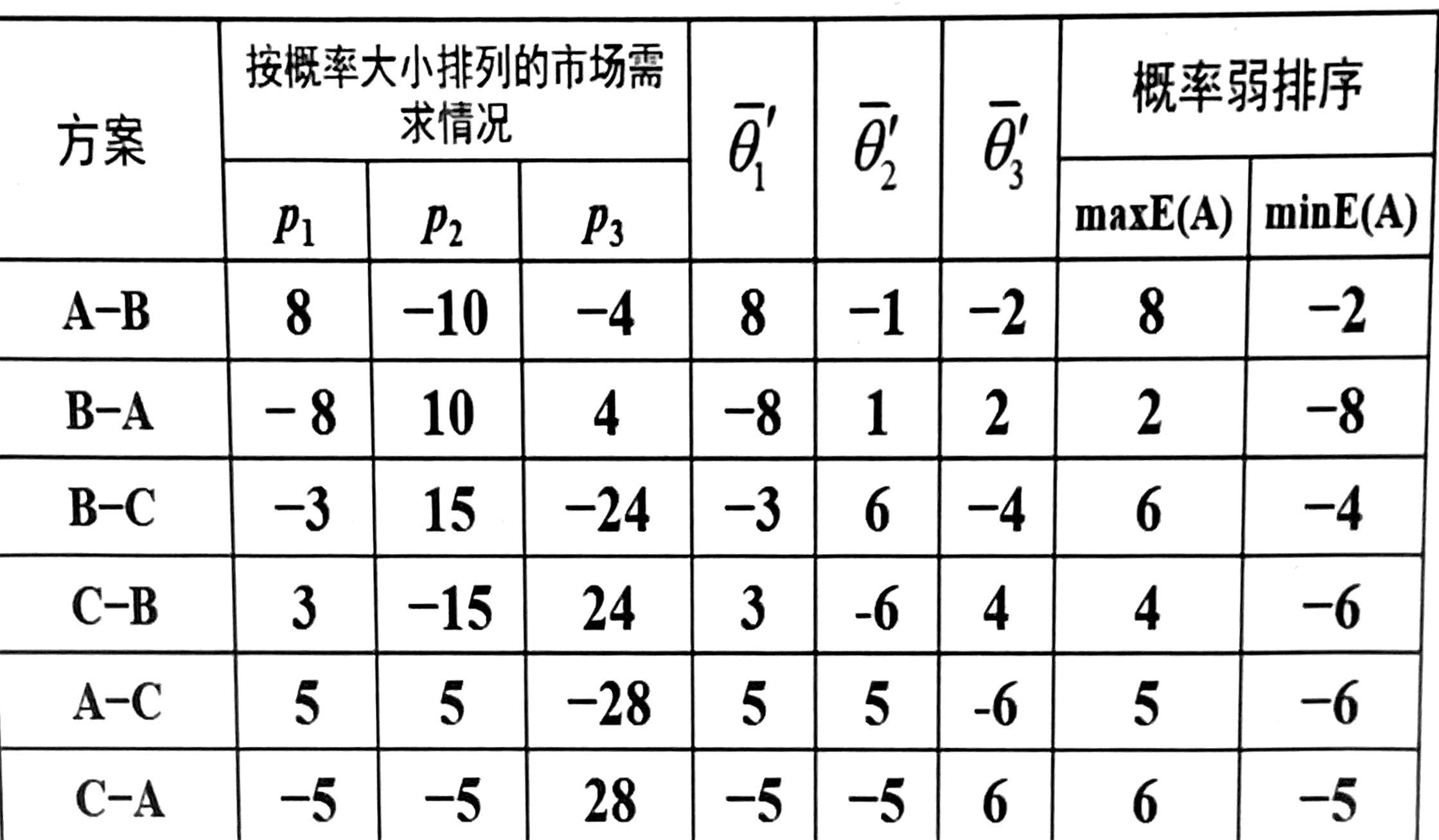
方案$A_i$相对于其他两个方案的优势程度为:
$$\sum_{j\ne i}(\max E(A_i-A_j)+\min E(A_i-A_j))$$
则方案$A$的优势程度为:
$\max E(A-B) + \min E(A-B) + \max E(A-C) + \min E(A-C) = 8+(-2)+5+(-6)=5$
同理可算出方案$B$的优势程度为$-4$,方案$C$的优势程度为$-1$
马尔可夫决策
没讲
效用理论及其在决策中的应用
效用的概念
设$C$表示决策者选择某一方案后,其产生的后果所构成的集合,集合的元素用$C_1,C_2,\cdots,C_n$表示,$p_i$是$C_i$发生的概率,$i=1,2,\cdots,n$,且$\sum\limits_{i=1}^n p_i=1$。以$P$表示后果的概率分布,并记$P=(p_1,C_1;p_2,C_2;\cdots;p_n,C_n)$,称为展望。所有展望构成的集合,称为展望集,用$\mathscr{F}$表示。$\mathscr{F}$中的各个元素之间有优先关系,例如$P_1$优于$P_2$,$P_2$优于$P_3$,这种优先关系记为:$P_1 \succ P_2 \succ P_3$。还有一种关系,称为优于或无差异于关系,记为$P_1 \succeq P_2$。若$P_1 \sim P_2$则称$P_1$与$P_2$无差异。
定义:设$u$是定义在集合$\mathscr{F}$上的实值函数,如$u$满足下述两个条件:
1.函数$u$在$\mathscr{F}$上的“优于或无差异于”一致,也就是说:
2.$u$在$\mathscr{F}$上是线性函数,即若$p_1,p_2 \in\mathscr{F}, 0\leq \lambda \leq 1$,有$$u(\lambda P_1+(1-\lambda ) P_2)=\lambda u(P_1) + (1-\lambda )u(P_2)$$
则称$u$是定义在$\mathscr{F}$上的效用函数。此定义可推广到更一般的情况,即若$P_i \in \mathscr{F}$,且$\lambda_i \geq 0,i=1,2,\cdots,m , \sum\limits_{i=1}^m \lambda_i=1$,则有
$$u(\sum\limits_{i=1}^m\lambda_i P_i)=\sum\limits_{i=1}^m \lambda_i u(P_i)$$
效用测定及效用曲线的制作
可以采用心理试验的方法打通过问答形式画出效用曲线,具体步骤如下:
1.确定效用的尺度范围
假定决策者有一幸运机会,可自由选择两周收入方案之一:
方案A:以0.5的概率得到300元,0.5的概率得到0元
方案B:稳拿50元
在这两个方案面前,决策者的最大收益是得到$300$元,效用最大,故取$u(300)=1$,最小的收益为$0$元,效用最小,故取$u(0)=0$
第二步:确定0元和300元中间的一个效用值,并对决策者进行问答,以测定决策者对不同方案的反应。
问:你认为方案B比方案A更稳妥吗?
答:是
这说明$50$元的效用值大于方案$A$的效用值,即$u(50)>u(A)$
将方案$A$改为以0.7的概率得300元,以0.3的概率的0元,其余不变。
问:你还愿意选$B$吗?
答:愿意
这说明$50$元的效用值仍大于方案$A$的效用值
再将方案$A$改为以0.8的概率得300元,0.2的概率获得0元,方案B不变。
问:你选择A还是B
答:无所谓
这说明$A$,$B$是等效用的,即$u(50)=u(A)$,而方案$A$的期望效用值为$0.8\times u(300)+0.2 \times u(0) = 0.8$,所以$u(50)=0.8$
第三步:确定50元与300元之间的一个点的效用值,假定确定了$u(100)=0.94$
第四步:确定0元与50元之间一个点的效用函数值,假定确定了$u(20)=0.56$
这样我们有5个点的效用函数值,分别为$u(0)=0,u(20)=0.56,u(50)=0.8,u(100)=0.94,u(300)=1$
可以绘出如下曲线:
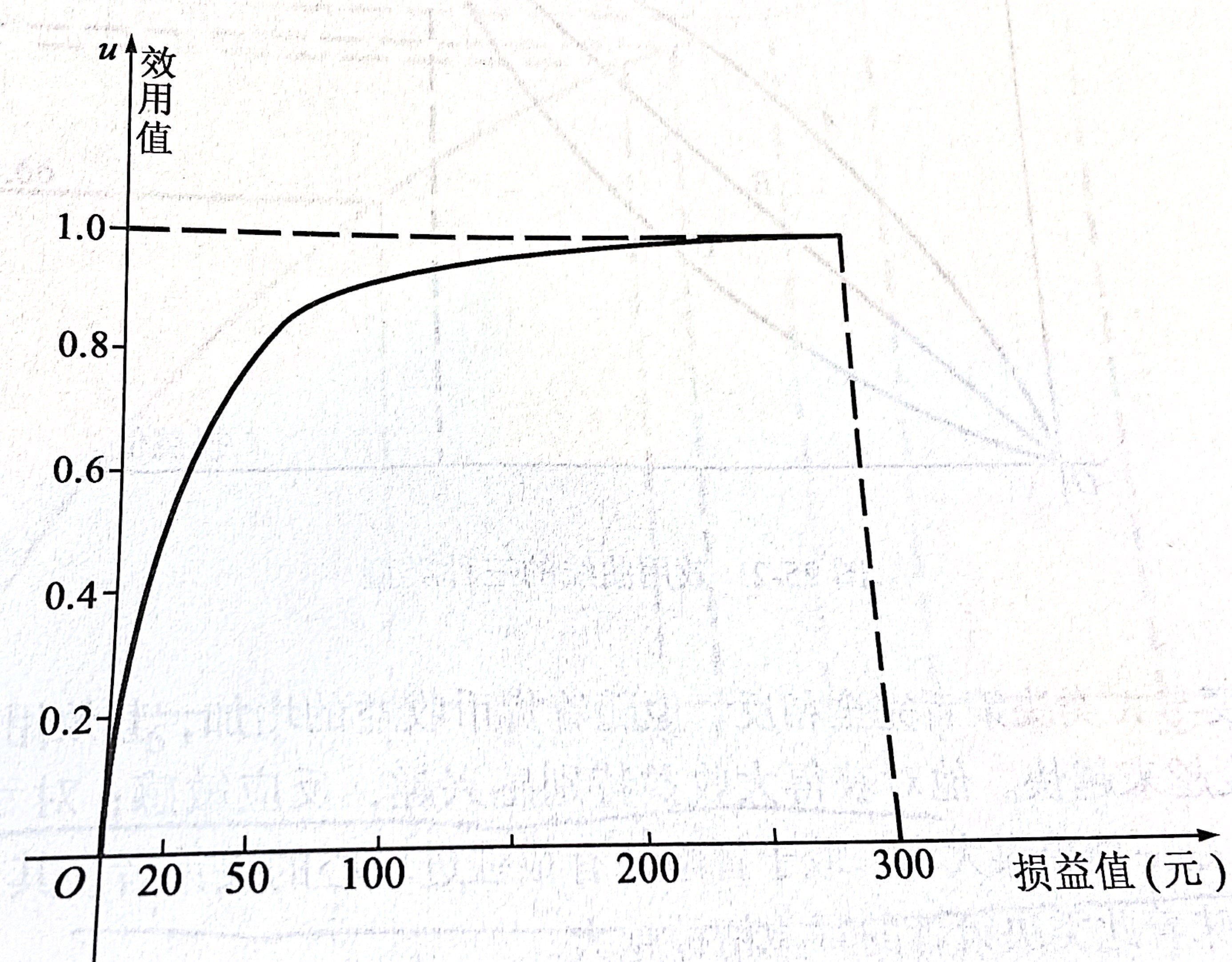
效用曲线的分类即效用决策准则
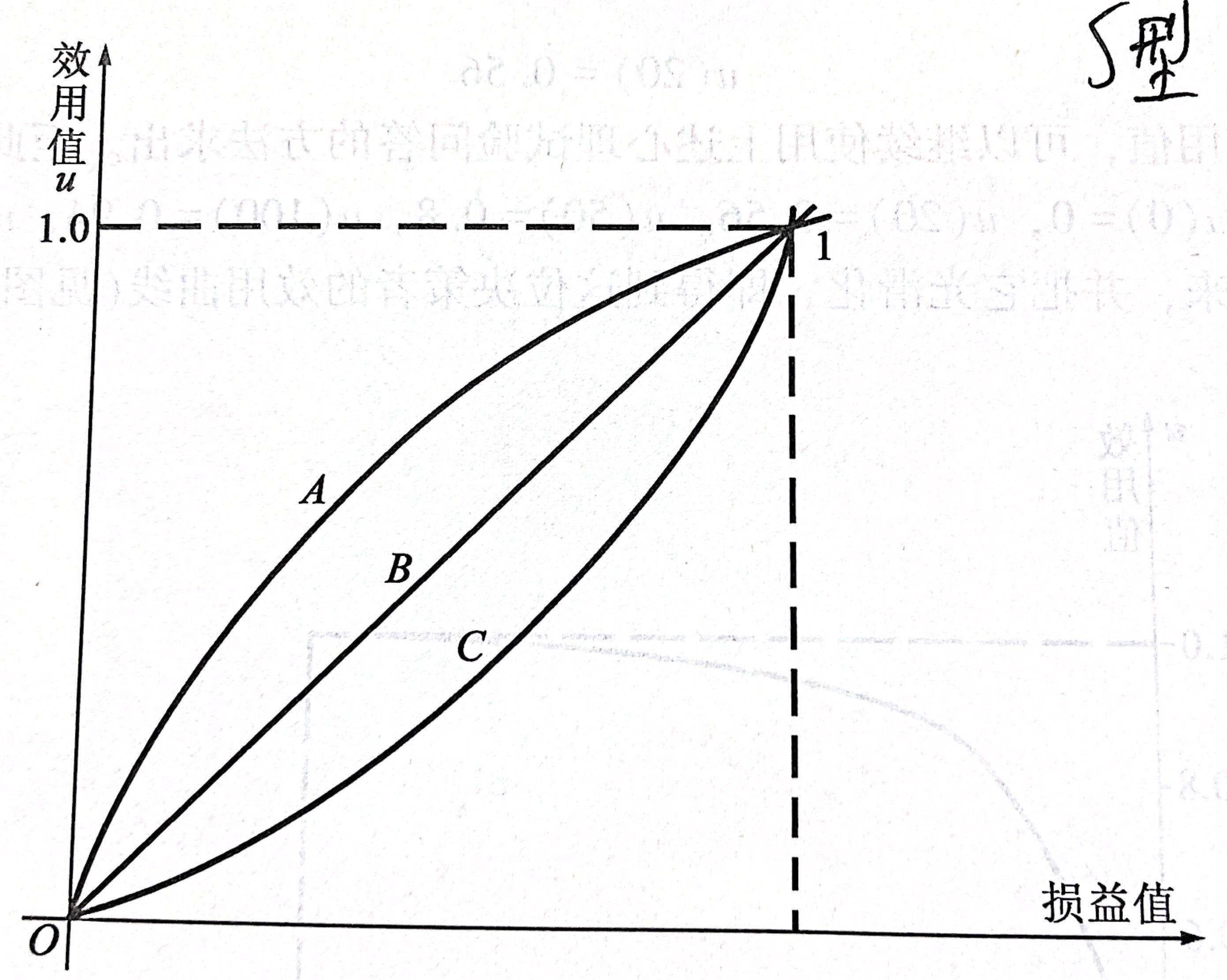
效用曲线的类型一般分为三种:
A类效用曲线,是一种保守型效用曲线,它表示决策者对货币收入的态度是,效用值随货币收入的增加而递增,但其实递增的速度越来越慢。这类决策者对损失较为敏感,而对收益的迅速增加,则反应比较迟缓,是一种不求大利,但求稳妥,小心谨慎,避免风险的风险厌恶者。这种效用曲线的特点是呈上凸型。
B类效用曲线,是一种风险中立者的效用曲线。他的决策准则就是期望收益最大。其曲线的特点是呈上升直线。
C类效用曲线,是一种冒险型的效用曲线,表示决策者在随着货币收益增加,其效用值也跟着递增,而且递增的速度越来越快。这种效用曲线的特点是呈下凸型。
例子
某公司准备经营某类商品,拟定了三种经营方案,未来市场有畅销、平销和滞销三种可能,市场状态和各方案的损益值如表所示。试用效用准则求出最优方案。求解步骤如下:

step1: 根据3.2的方法,做出决策者的效用曲线如下:
| 损益值 | -10 | -2 | 3 | 4 | 6 | 8 | 12 |
|---|---|---|---|---|---|---|---|
| 效用值 | 0 | 0.66 | 0.85 | 0.88 | 0.94 | 0.97 | 1.0 |
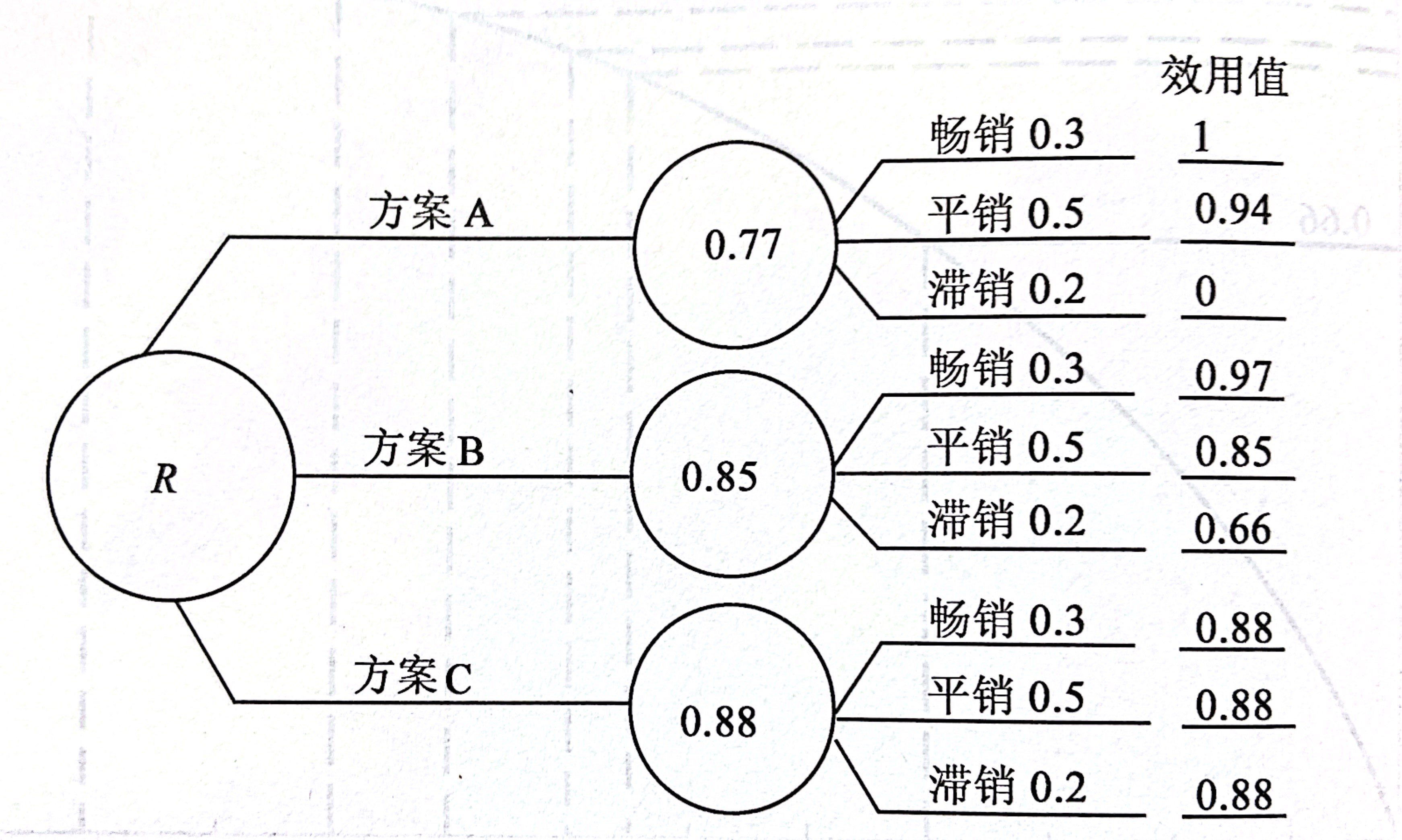
step2: 根据上表中的数据,分别计算A、B、C的期望效用值,得到:
方案A的期望效用值为$u(12)\times 0.3 + u(6)\times 0.5 + u(-10)\times 0.2 = 0.77$
方案B的期望效用值为$u(8)\times 0.3 + u(3)\times 0.5 + u(-2)\times 0.2 = 0.85$
方案C的期望效用值为$u(4)\times (0.3+0.5+0.2) = 0.88$
step3:运用决策树技术进行决策,从右往左计算出各方案的期望效用值,并填入圆圈内,再进行比较,即选择效用最大的方案作为最优方案。本例中方案C为最优方案。
对策论原理及其应用
对策论基本概念
局中人,策略集,支付函数
一般用$G=\{I,S,P\}$表示,其中$I$为局中人集合,$S$为策略空间,$P$代表支付函数。
若$S^*=(S_1^*,S_2^*,\cdots,S_n^*)\in S$,能使 $P(S_1^*,S_2^*,\cdots,S_n^*)$ 满足某种性质和条件,则称$S^*$为$G=\{I,S,P\}$在此意义的均衡解,称$S^*$为$S$中的一个均衡点,并称 $P(S_1^*,S_2^*,\cdots,S_n^*)$ 为相应的均衡支付。
矩阵对策
两人有限零和对策
有鞍点的对策
局中人有两个,记为$A,B$,$A$有$m$中策略,用$\alpha_1,\alpha_2,\cdots, \alpha_m$表示,$B$有$n$中策略,用$\beta_1,\beta_2,\cdots , \beta_n$表示。以$S_1$代表$A$的策略集,$S_2$代表$B$的策略集,$(\alpha_i,\beta_j)$构成局势,局势集合用$S$表示。
局中人$A$的支付矩阵记为$p_{ij}$,则矩阵
$$
P=
\left(
\begin{matrix}
p_{11} & p_{12} & \cdots & p_{1n} \\
p_{21} & p_{22} & \cdots & p_{2n} \\
\vdots & \vdots & & \vdots \\
p_{m1} & p_{m2} & \cdots & p_{mn} \\
\end{matrix}
\right)
$$
记$I=\{A,B\},S=\{S_1,S_2\}$
则$G=\{I,S,P\}$构成矩阵对策模型。
局中人$A$的最稳妥策略为$\max\limits_{i}\min\limits_{j} p_{ij}$
局中人$B$的最稳妥策略为$\min\limits_{j}\max\limits_{i} p_{ij}$
若其有鞍点,则满足$\max\limits_{i}\min\limits_{j} p_{ij}=\min\limits_{j}\max\limits_{i} p_{ij}$
无鞍点的对策
混合扩充,可以用线性规划求解。
局中人$A$对应的线性规划为
$
\begin{cases}
\min & \sum\limits_{i=1}^m x_i \\
s.t. & \sum\limits_{i=1}^m p_{ij}x_i \geq 1 , ~~ j=1,2,\cdots , n \\
& x_i \geq 0 , ~~~~~ i=1,2,\cdots,m \\
\end{cases}
$
局中人$B$对应的线性规划为
$
\begin{cases}
\max & \sum\limits_{j=1}^n y_j \\
s.t. & \sum\limits_{j=1}^n p_{ij}y_j \leq 1 , ~~ i=1,2,\cdots,m \\
& y_j \geq 0 , ~~~~~ j=1,2,\cdots , n \\
\end{cases}
$
并且设$\frac{1}{V}=\sum\limits_{i=1}^m x_i = \sum\limits_{j=1}^n y_j$,则 $X^* = V(x_1,x_2,\cdots, x_m), Y^* = V(y_1,y_2,\cdots , y_n)$是矩阵对策$\Gamma=\{S_1,S_2;A\}$的平衡局势,$V$是$\Gamma$的值。
eg:给出矩阵对策的支付矩阵为
$$
P= \begin{pmatrix}
1 & 3 & 3 \\
4 & 2 & 1 \\
3 & 2 & 2
\end{pmatrix}
$$
求最优策略和值
可以写出两个线性规划:
$
\begin{cases}
\min & z=x_1+x_2+x_3 \\
s.t. & x_1+4x_2+3x_3\geq 1 \\
& 3x_1+2x_2+2x_3 \geq 1 \\
& 3x_1+x_2+2x_3 \geq 1 \\
& x_1,x_2,x_3 \geq 0
\end{cases}
$
$
\begin{cases}
\max & w=y_1+y_2+y_3 \\
s.t. & y_1+3y_2+3y_3 \leq 1 \\
& 4y_1+2y_2+y_3 \leq 1 \\
& 3y_1+2y_2+2y_3 \leq 1 \\
& y_1,y_2,y_3 \geq 0
\end{cases}
$
解这对对偶规划,得到最优解:$X=(\frac{1}{7},0,\frac{2}{7}),~ Y=(\frac{1}{7},\frac{1}{7},\frac{1}{7}),~ V=\frac{7}{3}$
则$X^*=(\frac{1}{3},0,\frac{2}{3}), ~ Y^*=(\frac{1}{3},\frac{1}{3},\frac{1}{3})$
策略的优超
设矩阵对策$A=(a_{ij})_{m\times n}$,若
$a_{kj} \ge a_{ij}, j=1,2,\cdots, n$,则称局中人1的策略$k$优超于策略$l$
$a_{ik} \le a_{il}, i=1,2,\cdots, m$,则称局中人2的策略$k$优超于策略$l$
例:设矩阵$
A= \begin{pmatrix}
2 & 3 & -2 \\
-2 & 4 & 2 \\
1 & 2 & -3
\end{pmatrix}
$。
考虑第一行和第三行,局中人1绝对不会采取策略3,于是我们说对局中人1来说,策略1优超于策略3。
考虑第二列和第三列,局中人2绝对不会采取策略2,于是我们说对局中人2来说,策略3优超于策略2。
$2\times n $ 或 $m \times 2$类型的矩阵对策平衡局势的求法
$2\times n$类型的矩阵对策
Step1: 平面直角坐标系中做两条直线:$I:x=0$以及$II:x=1$
Step2: 在直线$I$处按照第二行矩阵的值标纵坐标,在直线$II$处按矩阵第一行的值标纵坐标;其意义是当局中人一采用某种纯策略时,局中人二各策略的赢得值。
Step3: 按列的方向将各对应纵坐标连成直线。
Step4: 令$0<x<1$,即局中人一采用混合策略时,找出线段中最小的纵坐标的若干条形成的折线,再在此折线上取最大值即可。
Step5: 通过交点确定$X^*$
Step6: 通过互补松紧条件确定$Y^*$
eg:求下面矩阵对策的平衡局势
$$
P= \begin{pmatrix}
2 & 3 & 11 \\
7 & 5 & 2
\end{pmatrix}
$$
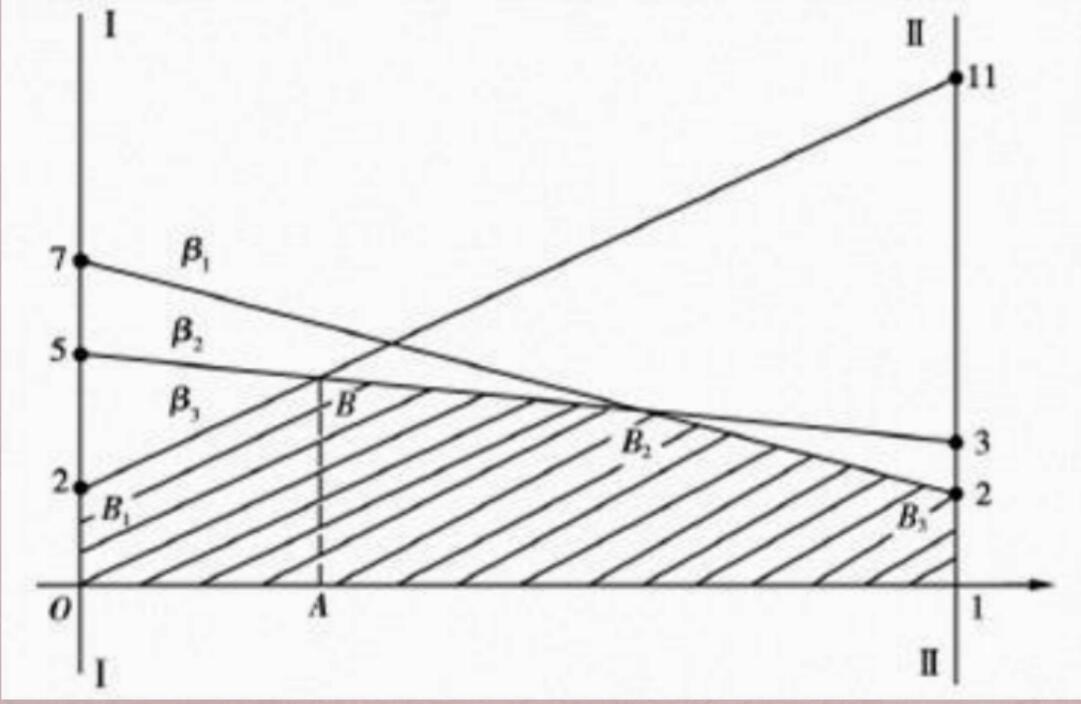
作图如上,可以列方程组:
$
\begin{cases}
11x+2(1-x)=V \\
3x+5(1-x)=V \\
\end{cases}
$
解得$x=\frac{3}{11}$
则$X^*=(\frac{3}{11},\frac{8}{11})$
再来求解$Y$,可以列出方程组
$
\begin{cases}
2y_1^*+3y_2^*+11y_3^*=V \\
7y_1^*+5y_2^*+2y_3^*=V \\
y_1^*+y_2^*+y_3^*=1
\end{cases}
$
由互补松紧条件知$y_1^*=0$,则可求解出$y_2^*=\frac{9}{11},y_3^*=\frac{2}{11}$
$m\times 2$类型的矩阵对策
与上面类似,
Step1: 平面直角坐标系中做两条直线:$I:y=0$以及$II:y=1$
Step2: 在直线$I$处按照第二列矩阵的值标纵坐标,在直线$II$处按矩阵第一列的值标纵坐标;其意义是当局中人二采用某种纯策略时,局中人一各策略的赢得值。
Step3: 按行的方向将各对应纵坐标连成直线。
Step4: 令$0<x<1$,即局中人二采用混合策略时,找出线段中最大的纵坐标的若干条形成的折线,再在此折线上取最小值即可。
Step5: 通过交点确定$Y^*$
Step6: 通过互补松紧条件确定$X^*$
eg:求下面矩阵对策的平衡局势
$$
P= \begin{pmatrix}
2 & 7 \\
6 & 6 \\
11 & 2
\end{pmatrix}
$$
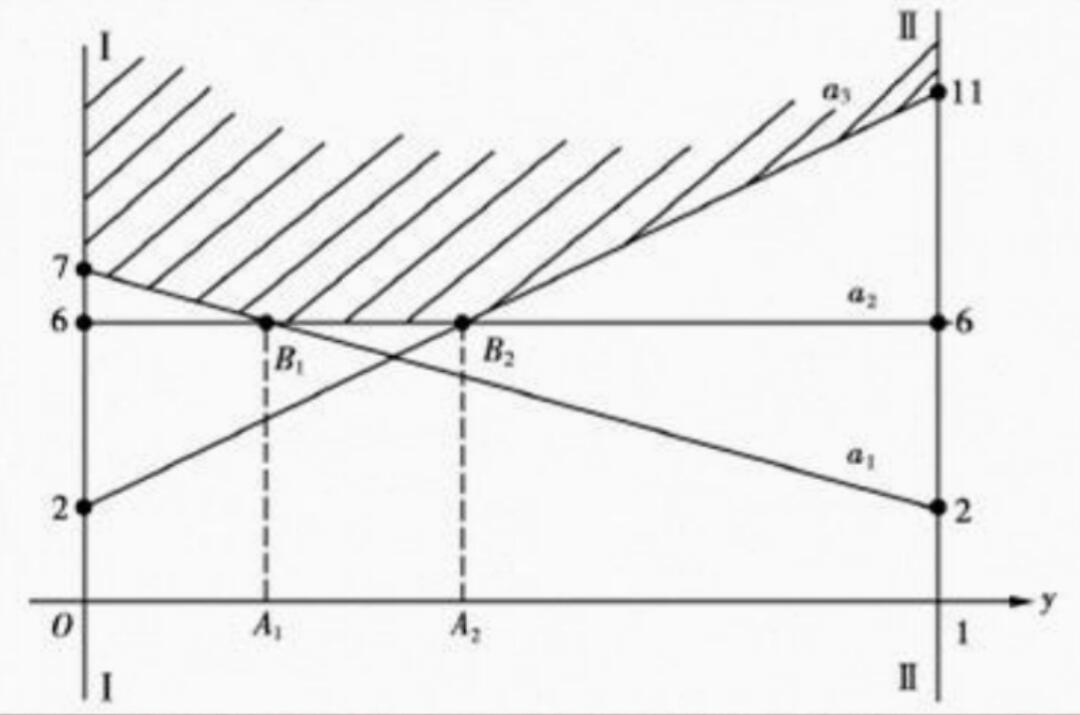
作图如上,按照和上例类似的方法即可求出平衡局势。
连续对策
基本概念
设两人进行对策,每个人的对策均为$[0,1]$的单位区间,当局中人1在$[0,1]$选取一个点$x$,局中人2在$[0,1]$选取一个点$y$,此时局中人1的支付函数为$P(x,y)$,局中人2的支付函数为$-P(x,y)$。称这类对策为两人无限零和对策(对抗对策)$P(x,y)$称为局中人1的支付函数。
局中人1期望达到的状态,即最多获得$\max\limits_{x \in [0,1]} \min\limits_{ y\in [0,1]} P(x,y)$
局中人2期望达到的状态,即最多失去$\min\limits_{y \in [0,1]} \max\limits_{x \in [0,1]} P(x,y)$
如果$\max\limits_{x \in [0,1]} \min\limits_{ y\in [0,1]} P(x,y) = \min\limits_{y \in [0,1]} \max\limits_{x \in [0,1]} P(x,y) $则称该矩阵对策有解,上式共同的值称为对策的值,记为$V$
但是并非所有对抗对策都有平衡局势,于是我们要引入混合扩充的概念。
混合扩充
设$F(x)$为$[0,1]$上的一个分布函数,并且记$[0,1]$上的所有分布函数组成的集合为$D$
设局中人1选取混合策略$F(x)\in D$,局中人2选取混合策略$G(y)\in D$,于是局中人1的对策期望值为$\int_0^1 \int _0^1 P(x,y)dF(x)dG(y)$,这里的积分为Stieltjes积分。
Th:设单位正方形上对策的支付函数$P(x,y)$是$[0,1]\times [0,1]$上的连续函数,则下述$v_1$和$v_2$存在且相等。
$v_1 = \max\limits_{F\in D} \min\limits_{G\in D}\int_0^1 \int _0^1 P(x,y) dF(x) dG(y)$
$v_2 = \min\limits_{G\in D} \max\limits_{F\in D} \int_0^1 \int_0^1 P(x,y) dF(x) dG(y)$
Th:设$P(x,y)$为连续对策的支付函数,又设实数$v$及分布函数$F_0(x)$和$G_0(y)$,对$[0,1]$上的任何$x,y$,有$\int_0^1P(x,y)dG_0(y) \le v \le \int_0^1 P(x,y)dF_0(x)$,其中$v$是对策的值,$F_0(x),G_0(y)$分别是局中人1和局中人2的最优策略。
eg:设连续对策的支付函数为$P(x,y)=\frac{3}{3+2(x-y)^2} , 0\le x \le 1, 0 \le y \le 1$,求证:对策的值为$\frac{6}{7}$,且$I_{\frac{1}{2}}(x)$和$\frac{1}{2}I_0(y)+\frac{1}{2} I_1(y)$为局中人1和局中人2的最优策略。
只需证明$\int_0^1 \frac{3}{3+2(x-y)^2} d(\frac{1}{2}I_0(y)+\frac{1}{2} I_1(y)) \le \frac{6}{7} \le \int_0^1 \frac{3}{3+2(x-y)^2} d(I_{\frac{1}{2}}(x))$即可。
而$\int_0^1 \frac{3}{3+2(x-y)^2} d(\frac{1}{2}I_0(y)+\frac{1}{2} I_1(y)) = \frac{1}{2}\frac{3}{3+2x^2} + \frac{1}{2}\frac{3}{2(x-1)^2}$
随机型需求的投资项目决策
项目选择准则
在正态需求的情况下,对互斥方案的择优标准是什么?我们提出以下几条供决策者参考。
- 盈利的可能性要有较大的把握,即盈利在99%以上
- 企业经营实现最低成本的可能性最大
- 期望成本最低
- 期望利润最大
以上四条可归结为成本和利润两个方面。此外,还要考虑设备利用率和满足市场需求方面的参考标准,这就是: - 设备利用率在80%以上的可能性不低于75%
- 满足客户需求的可能性在80%以上。
一个例子
现通过一实例,给出一个互斥的项目建设方案的具体选优决策方法。
假设某种产品的需求服从正态分布,其平均需求量为120万件,标准差为20万件,单件售价20万元。
方案甲:固定成本为400万元,使用自动化装置,年最大生产能力为130万件,每件可变成本为11.5元,规模属中等。
方案乙:固定成本为200万元,不采用自动化装置,年最大生产能力为100万件,每件可变成本为15元,属于小型规模
方案丙:采用高度自动化装置,固定成本为600万元,年最大生产能力为160万件,每件可变成本为10元,属于大型规模。
在最优化的准则下,怎么求出最优的建设方案?一下是可以采取的具体方法:
进行线性盈亏分析。设
$Q$为产量,$TR$为总收益,$TC$为总成本,$F$为固定资本,$C_v$为可变成本,$p$为单件售价
总收益$TR=pQ$
总成本$TC=F+C_vQ$
可以算出盈亏平衡点的产量:
$
\begin{cases}
Q_甲^*=\frac{400}{20-11.5}=47.06 ~~ (万件) \\
Q_乙^*=\frac{200}{20-15}=40 ~~ (万件) \\
Q_丙^*=\frac{600}{20-10}=60 ~~ (万件)
\end{cases}
$
由上述计算,可得到$Q_乙^*<Q_甲^*<Q_丙^*$
企业乙有较低的盈亏平衡点。但是,他开始盈利之后,利润增长的速度比甲、丙都慢。
企业丙有较高的固定成本,因而盈亏平衡点比甲、乙都高。但是其一旦超过盈亏平衡点,利润将迅速增加。
企业甲则处于乙、丙之间。
可见,上述方案各有利弊,下面将从本实例继续展开分析。
盈利可能性计算
设$p(Q)$为需求量$Q$的概率密度,则有概率密度函数
$$p(Q)=\frac{1}{20\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{Q-120}{20})^2}$$
盈利的可能性
方案甲:$P(Q>Q_甲^*)=P(Q>47)=\int_{47}^{\infty}p(Q)dQ=99.95\%$
方案乙:$P(Q>Q_乙^*)=P(Q>40)=\int_{40}^{\infty}p(Q)dQ=99.99\%$
方案丙:$P(Q>Q_丙^*)=P(Q>60)=\int_{60}^{\infty}p(Q)dQ=99.86\%$
盈利300万元以上的可能性计算
首先求出相应的产量公式
$20Q-F-C_vQ > 300 \Rightarrow Q > \frac{300+F}{20-C_v}$
从而盈利300万元以上的可能性为:$P(Q>\frac{300+F}{20-C_v})=\int_{\frac{300+F}{20-C_v}}^{+\infty}p(Q)dQ$
可以算出以下各概率
方案甲:$P(Q>\frac{300+400}{20-11.5})=\int_{82.35}^{+\infty}p(Q)dQ=97\%$
方案乙:盈利300万元以上,其产量$Q$至少应为100万件,但是方案乙的最大产量仅为100万件,故盈利300万元以上的概率为0。
方案丙:$P(Q>\frac{300+600}{20-10})=\int_{90}^{+\infty}p(Q)dQ=93.3\%$
盈利400万元以上的可能性计算
方案甲:$P(Q>\frac{400+400}{20-11.5})=\int_{800/8.5}^{+\infty}p(Q)dQ=89.5\%$
方案乙:概率为0。
方案丙:$P(Q>\frac{400+600}{20-10})=\int_{100}^{+\infty}p(Q)dQ=84.1\%$
期望利润计算
由于总收益和总成本均是需求量的函数,故总利润$TR-TC=20Q-F-C_vQ=(20-C_v)Q-F$
方案甲:由于设备最大生产能力为每年130万件,故它的利润计算公式为:
$
TR_甲-TC_甲=
\begin{cases}
(20-C_{v甲})Q-F_甲 & 当需求量Q\le 130时 \\
(20-C_{v甲})\times 130-F_甲 & 当需求量Q>130时
\end{cases}
$
期望利润为
$$E(TR_甲-TC_甲)=\int_{-\infty}^{130}(20-11.5)Qp(Q)dQ+\int_{130}^{+\infty}(20-11.5)\times 130 p(Q)dQ-400 =586.408(万元)$$
同理可算出乙的期望利润为$291.87$万元,丙的期望利润为$598.4$万元。
期望成本计算
成本公式$TC=F+C_vQ$
方案甲的成本计算公式为$
TC_甲=
\begin{cases}
400+11.5Q & 当需求量Q\le 130时 \\
400+11.5\times 130 & 当需求量Q>130时
\end{cases}
$
故方案甲打的期望成本为
$$ETC_甲=400+\frac{11.5}{20\sqrt{2\pi}}\int_{-\infty}^{130}Qe^{-\frac{1}{2}(\frac{Q-120}{20})^2}dQ +\frac{1495}{20\sqrt{2\pi}}\int_{130}^{+\infty}Qe^{-\frac{1}{2}(\frac{Q-120}{20})^2} dQ = 1591.837(万元) $$
同理可算出方案乙的期望成本为$1675.1$万元,方案丙的期望成本为$1798.7$万元。
实现最低成本的可能性计算
首先将三种方案的成本直线绘制在同一图形上,如图所示
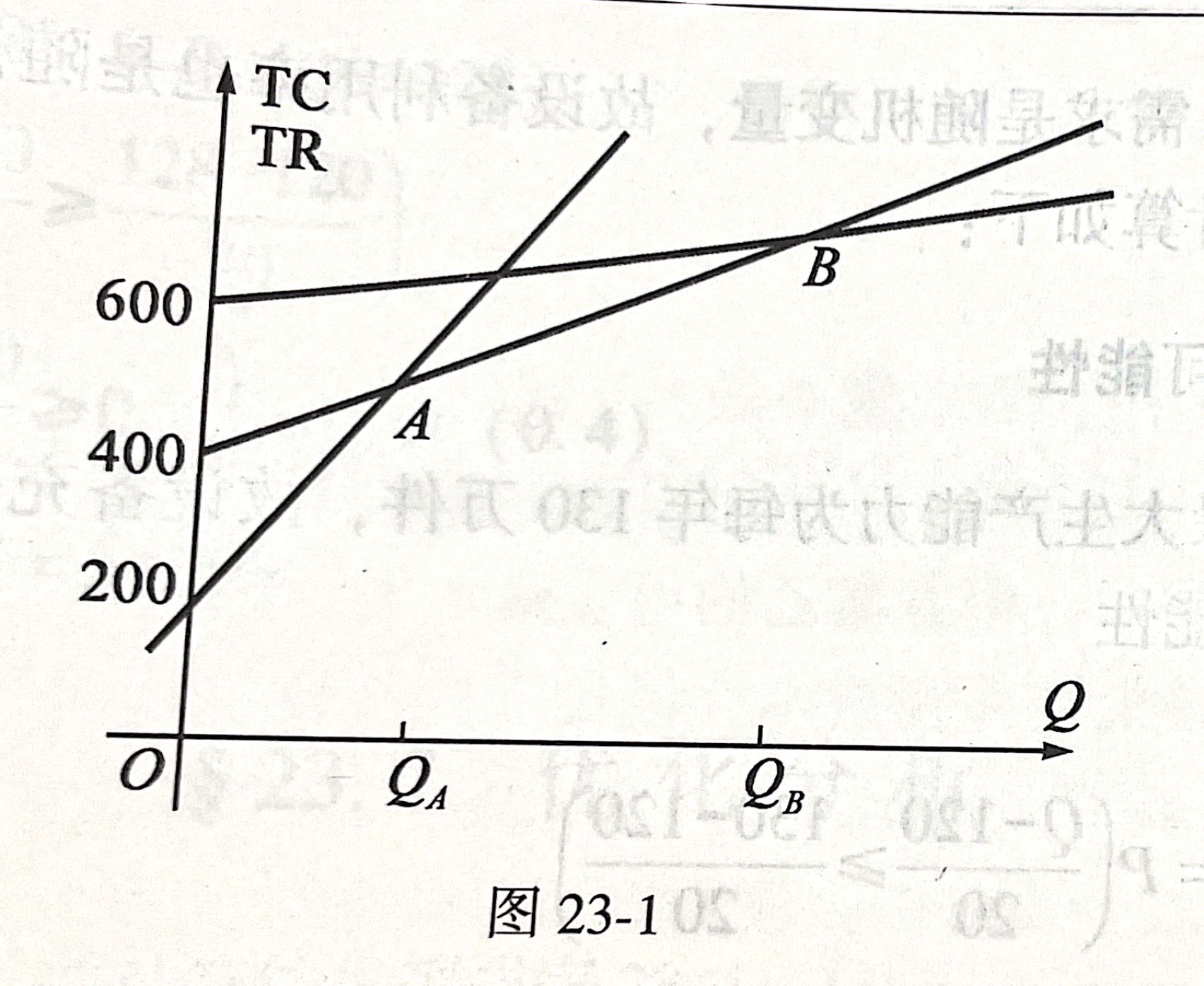
$TC_甲$与$TC_乙$相交于$A$点,故在交点$A$处有:$TC_乙=TC_甲$,$F_乙+C_{v乙}Q=F_甲+C_+{v甲}Q$
即$Q_A=\frac{F_甲-F_乙}{C_{v乙}-C_{v甲}}=\frac{400-200}{15-11.5}=57.14$(万件)
同理,在$B$处有$TC_甲=TC_丙$,可以计算出$Q_B=133.3$(万件)
$Q_A$与$Q_B$将产量分为三部分,从图形上看,当$Q\le Q_A$时,方案乙有最低成本,当$Q_A<Q<Q_B$时,方案甲有最低成本;当$Q>Q_B$时,方案丙有最低成本。实现最低成本的可能性为:
方案甲:$P(Q_A<Q<Q_B)=P(57.14<Q<133.3) = \int_{57.14}^{133.3}p(Q)dQ = 0.741$
方案乙:$P(Q<Q_A)=P(Q<57.14)=\int_{-\infty}^{57.14}p(Q)dQ = 0.000135$
方案丙:$P(Q>Q_B)=P(Q>133.3)=\int_{133.3}^{+\infty} p(Q)dQ = 0.2578$
设备利用率计算
设备充分利用的可能性
方案甲:设备的最大生产能力为每年130万件,故设备充分利用的可能性就是需求量不少于130万件的可能性,即
$P(Q\geq 130)=P(\frac{Q-120}{20}\geq \frac{130-120}{20}) = P(\frac{Q-120}{20}>0.5) = 1-\Phi(0.5) = 1-69.1\% = 30.9 \% $
同理可计算出方案乙的可能性为$84.1\% $ ,方案丙的可能性为$ 2.3 \%$
设备利用率大于80%的可能性
方案甲的可能性为
$P(Q\geq 130\times 0.8)= P(\frac{Q-120}{20}>-0.8) = \Phi(0.8) = 78.8\% $
同理可得方案乙的可能性为$97.7\% $,方案丙的可能性为$34.5 \% $
优化分析
可以从三方面来看:利润贡献分析,成本分析,设备使用率分析。
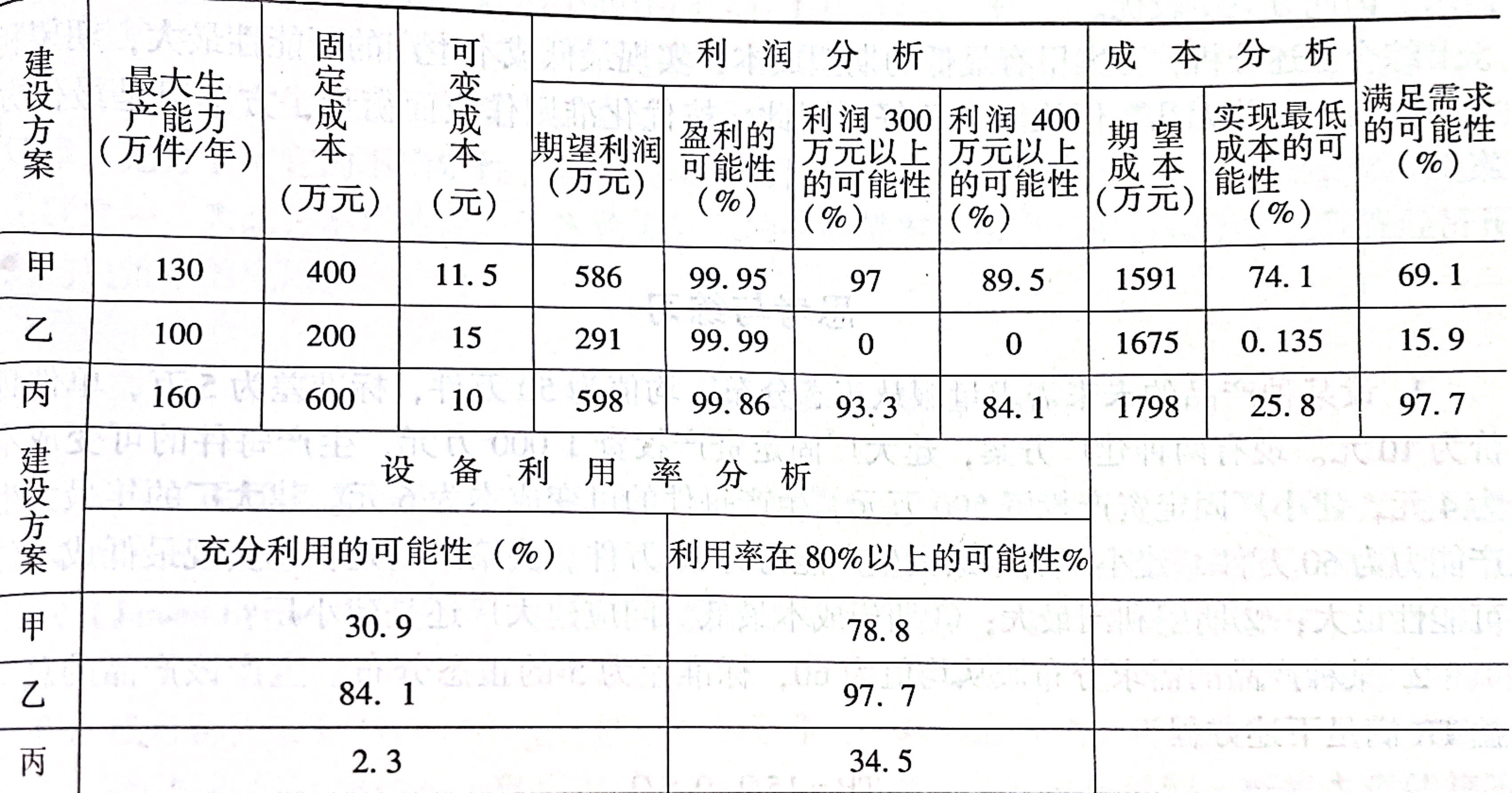
利润贡献分析
从表中可以看出,三种方案的 盈利可能性都在$99\% $以上,因而亏损的可能性很小。 利润在300万元以上的可能性,方案甲最高,从 期望利润来看,方案丙最高,但方案甲和方案丙差距不大。因此认为方案甲最优。
成本分析
从期望成本来看,方案甲有最低的 期望成本,实现最低成本生产的可能性为$74.1\% $,从此看出甲方案最优。
设备利用率分析
方案甲的设备充分利用概率在$30\% $以上,而且利用率在$80\% $以上的可能性在$78\% $以上。而方案乙的规模小,利用率比甲、丙方案都大,但方案乙的可变成本大,因而总成本高,从经济效益上看是不合算的。
另一方面,从满足需求来看,规模愈大,满足需求的可能性就愈大,但规模愈大,设备利用率就低。方案甲的满足需求的可能性占$69.1\% $,即在大多数情况下基本可以满足需求。
综合上述分析,方案甲有最低的期望成本,实现最低成本生产的可能性最大,期望利润与方案丙相差无几,但比方案乙好,因此,按优化准则作全面衡量,方案甲是最优方案。