单调栈好题
传送门
大致题意:给你$n\times n$的矩阵$A$,让你求矩阵中所有子矩阵的与$\&$和或$|$的和。
数据范围:$n\leq 2000,a_{i,j}\leq 2^{31}-1$
大致题解:拆位考虑,对于与运算,我们对每一个$a_{i,j}$计算以它为右下角的全1子矩阵个数,对于或运算,我们计算以$a_{i,j}$为右下角的全0子矩阵个数,然后用$i\times j$减去全0子矩阵的个数即可。
下面讨论怎么使用单调栈来维护以$a_{i,j}$为右下角的全1/0子矩阵个数。
预处理$s_{i,j}$为以$a_{i,j}$上方连续的1/0的个数,然后我们依次枚举一个点,计算以它为右下角的全1/0的子矩阵的个数。
我们设$f_{i,j}$是以$a_{i,j}$为右下角的全1/0子矩阵的个数,维护一个单调递增的栈,当未发生弹栈的时候,我们有
$$f_{i,j}=f_{i,j-1}+s_{i,j}$$
其中第一部分是从左边延伸过来的,第二部分是从$a_{i,j}$向上延伸的。
具体见图: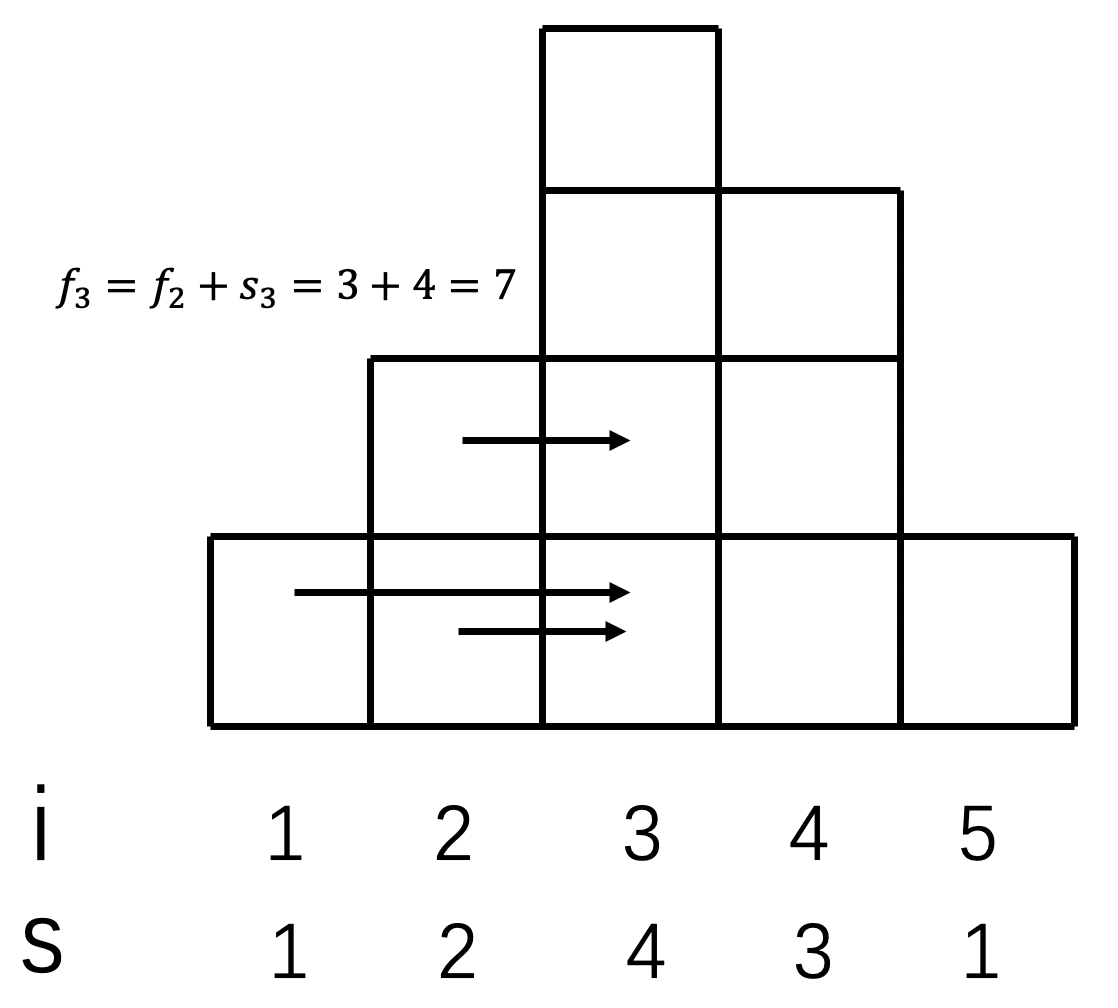
当发生弹栈的时候,意味着左边的延伸不过去了,需要减掉,我们有
$$f_{i,j}=f_{i,j}-(s_{i,j}-s_{i,st.top()})*(st.top()-st.(top-1)())$$
其中$st.(top-1)()$表示栈顶的下一个元素。
具体见图(3弹栈的时候):
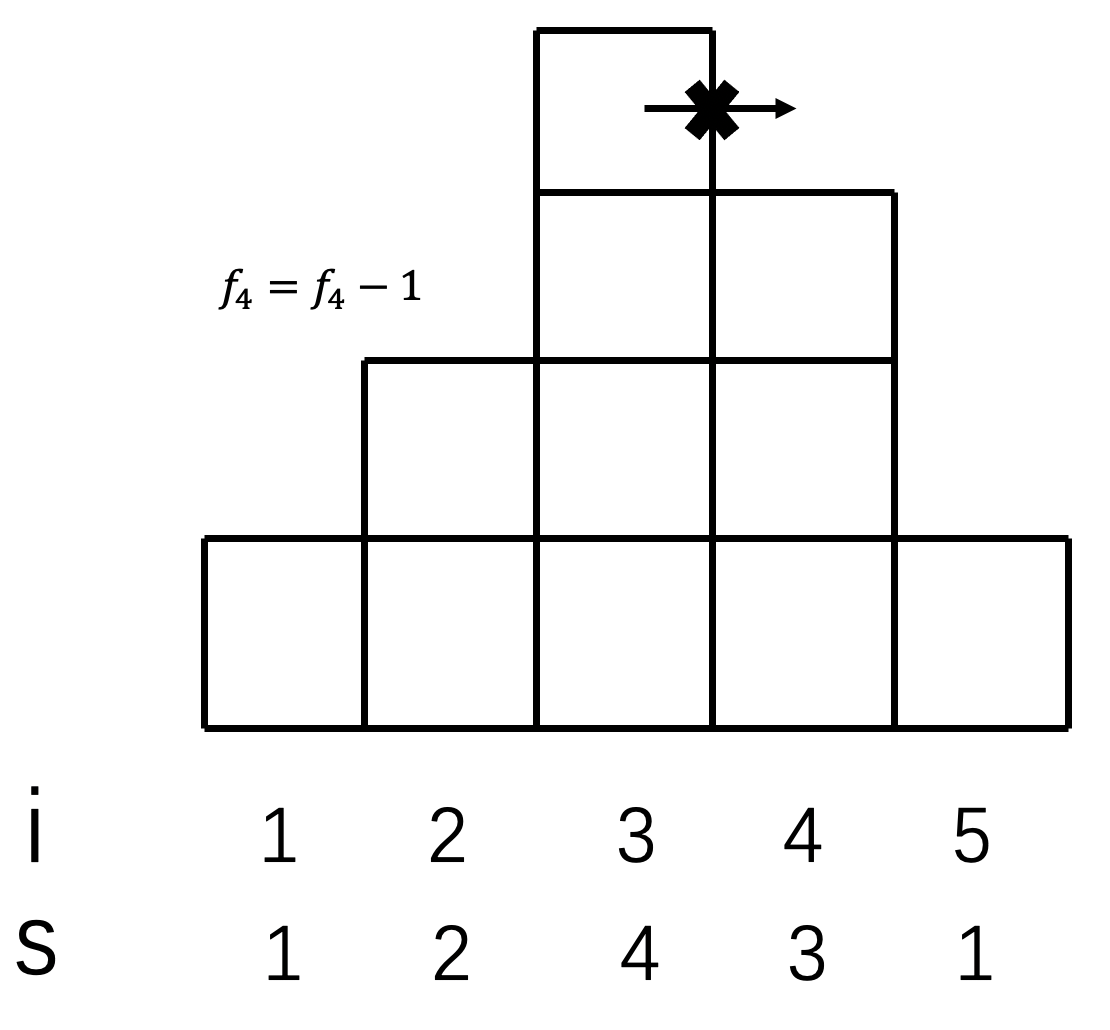
这样就维护了答案。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
| #pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include <algorithm>
#include <cassert>
#include <climits>
#include <cctype>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <fstream>
#include <functional>
#include <iomanip>
#include <iostream>
#include <map>
#include <queue>
#include <deque>
#include <set>
#include <stack>
#include <string>
#include <vector>
#define pb push_back
#define fi first
#define se second
#define IOS ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
#define mem(a,x) memset(a, x, sizeof(a))
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;
typedef double db;
typedef pair<ll, ll> P;
const double pi = acos(-1);
const ll mod = 1e9+7;
const ll INF = 2e9;
const int maxn=2000+10;
ll qp (ll a, ll b, ll mod)
{
ll ans = 1;
while (b)
{
if (b & 1)
ans = ans * a % mod;
a = a * a % mod;
b >>= 1;
}
return ans;
}
int n;
int a[maxn][maxn];
int up[maxn][maxn];
ll ans1,ans2;
int main()
{
IOS;
cin>>n;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
cin>>a[i][j];
for(int k=0;k<31;k++)
{
mem(up[0],0);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(a[i][j]&(1<<k))
up[i][j]=up[i-1][j]+1;
else
up[i][j]=0;
}
}
for(int i=1;i<=n;i++)
{
stack<int> s;
s.push(0);
up[i][0]=0;
up[i][n+1]=0;
ll bns=0;
for(int j=1;j<=n;j++)
{
bns+=up[i][j];
while(s.size()&&up[i][j]<up[i][s.top()])
{
int x = s.top();
s.pop();
bns=bns-(x-s.top())*(up[i][x]-up[i][j]);
}
s.push(j);
ans1=(ans1+(bns<<k))%mod;
}
}
mem(up[0],0);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if((a[i][j]&(1<<k))==0)
up[i][j]=up[i-1][j]+1;
else
up[i][j]=0;
}
}
for(int i=1;i<=n;i++)
{
stack<int> s;
up[i][0]=0;
up[i][n+1]=0;
s.push(0);
ll bns=0;
for(int j=1;j<=n;j++)
{
bns=bns+up[i][j];
while(s.size()&&up[i][j]<up[i][s.top()])
{
int x = s.top();
s.pop();
bns=bns-(x-s.top())*(up[i][x]-up[i][j]);
}
s.push(j);
ans2=(ans2+((1ll*i*j-bns)<<k))%mod;
}
}
}
cout<<ans1<<" "<<ans2<<endl;
return 0;
}
|

